Merge Intervals

Posted on

两个区间之间存在 6 种可能情况。取交集时，start = max(a.start, b.start); end = min(a.end, b.end)。

This pattern describes an efficient technique to deal with overlapping intervals. In a lot of problems involving intervals, we either need to find overlapping intervals or merge intervals if they overlap.

Given two intervals (“a” and “b”), there will be six different ways the two intervals can relate to each other: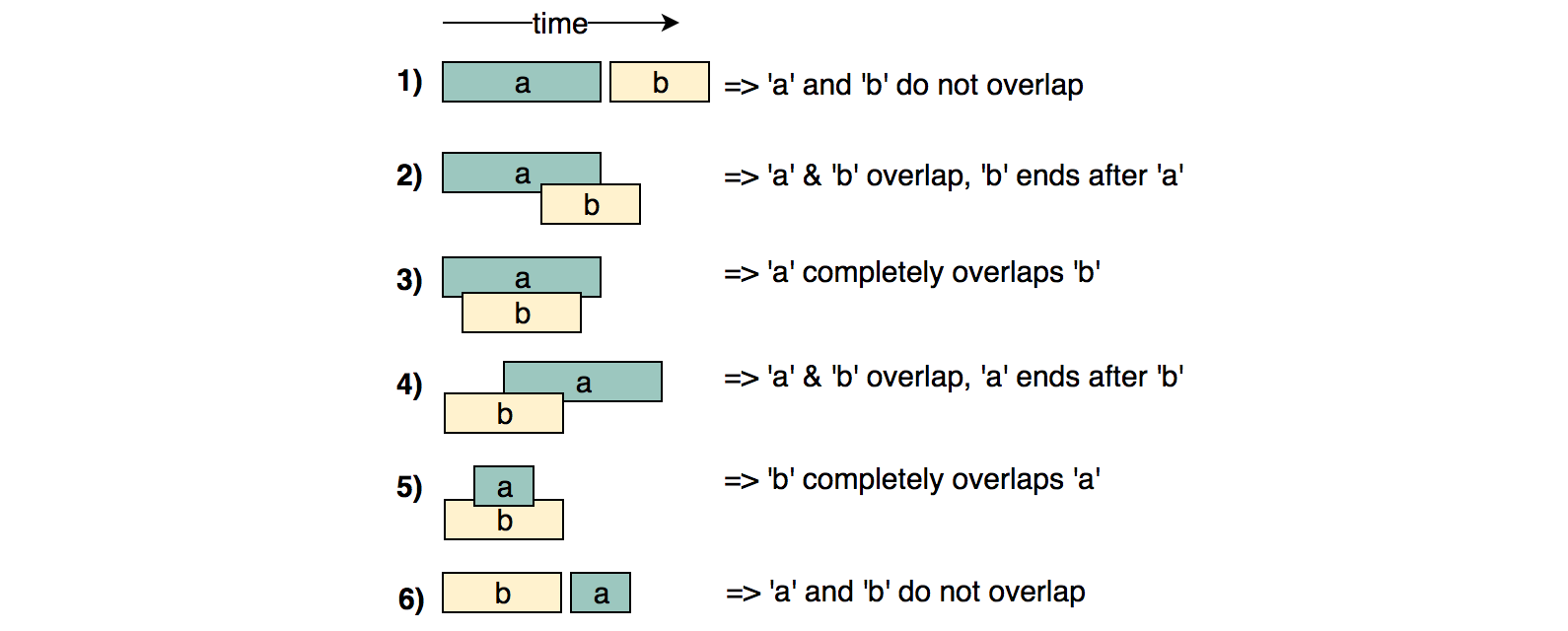

Understanding the above six cases will help us in solving all intervals related problems.

Snippets

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
n = len(intervals)
ans = []

i = 0
# case 1
while i < n and intervals[i][1] < newInterval[0]:
    ans.append(intervals[i])
    i += 1
# case 2-5
while i < n and intervals[i][0] <= newInterval[1]:
    newInterval[0] = min(newInterval[0], intervals[i][0])
    newInterval[1] = max(newInterval[1], intervals[i][1])
    i += 1
ans.append(newInterval)
# case 6
while i < n:
    ans.append(intervals[i])
    i += 1

return ans

LeetCode

56. Merge Intervals
57. Insert Interval
986. Interval List Intersections
435. Non-overlapping Intervals
253. Meeting Rooms II
1094. Car Pooling
759. Employee Free Time