基本流程
决策过程中提出的每个判定问题都是对某个属性的测试
考虑范围在上一次决策结果的限定范围之内
- 叶结点对应于决策结果
- 其他每个结点对应于一个属性测试
- 根结点包含样本全集
目的
决策树学习的目的是为了,产生一棵处理未见示例能力强的决策树。
遵循简单且直观的分而治之(divide-and-comquer)策略。
递归过程
三种情形会导致递归返回:
- 当前结点包含的样本全属于同一类别;
- 当前属性集为空,或是所有样本在所有属性上取值相同;
- 当前结点包含的样本集合为空;
划分选择
决策树学习的关键是,如何选择最优划分属性。
随着划分过程不断进行,结点的纯度(purity)越来越高。
信息增益
信息熵(information entropy)是度量样本集合纯度最常用的一种指标。
Ent(D) 的值越小,则 D 的纯度越高。
信息增益越大,使用属性a来进行划分所获得的纯度提升越大。
ID3 以信息增益为准则来选择划分属性。
增益率
信息增益准则对可取值数目较多的属性有所偏好。
增益率(gain ratio)准则对可取数目较少的属性有所偏好。
C4.5 使用增益率来选择最优划分属性。
启发式:
- 从候选划分属性中找出信息增益高于平均水平的属性;
- 从中选择增益率最高的;
基尼指数
基尼指数(Gini index)反映了从数据集 D 中随机抽取两个样本,其类别标记不一致的概率。
Gini(D) 越小,则数据集 D 的纯度越高。
CART 使用基尼指数来选择划分属性。
剪枝处理
剪枝(pruning)是决策树学习算法对付过拟合的主要手段。
- 预剪枝(prepruning):若当前结点的划分不能带来决策树泛化性能提升,则停止划分并将当前结点标记为叶结点。
- 后剪枝(postpruning):自底向上,若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升,则将该子树替换为叶结点。
预剪枝
仅有一层划分的决策树,亦称决策树桩(decision stump)。
显著减少了决策树的训练时间开销和测试时间开销。
后续划分有可能导致性能显著提高,禁止这些分支展开,带来了欠拟合的风险。
后剪枝
后剪枝决策树通常比预剪枝决策树保留了更多的分支。
训练时间开销比未剪枝和预剪枝都要大得多:
- 在生成完全决策树之后进行的;
- 要自底向上地对树中所有非叶结点进行逐一考察;
连续与缺失值
连续值处理
把区间的中位点作为候选划分点,选择使 Gain(D, a, t) 最大化的划分点。
与离散属性不同,该属性还可作为其后代结点的划分属性。
缺失值处理
现实任务中常会遇到不完整样本,即样本的某些属性值缺失。
有必要考虑利用有缺失属性值的训练样例来进行学习。
解决两个问题:
- 如何在属性值缺失的情况下进行划分属性选择:根据没有缺失值的样本子集来判断属性a的优劣;
- 给定划分属性,若样本在该属性上的值缺失,如何对样本进行划分:让同一个样本以不同的概率划入到不同的子结点去;
多变量决策树
决策树所形成的分类边界有一个明显的特点:轴平行(axis-parallel),即分类边界由若干个与坐标轴平行的分段组成。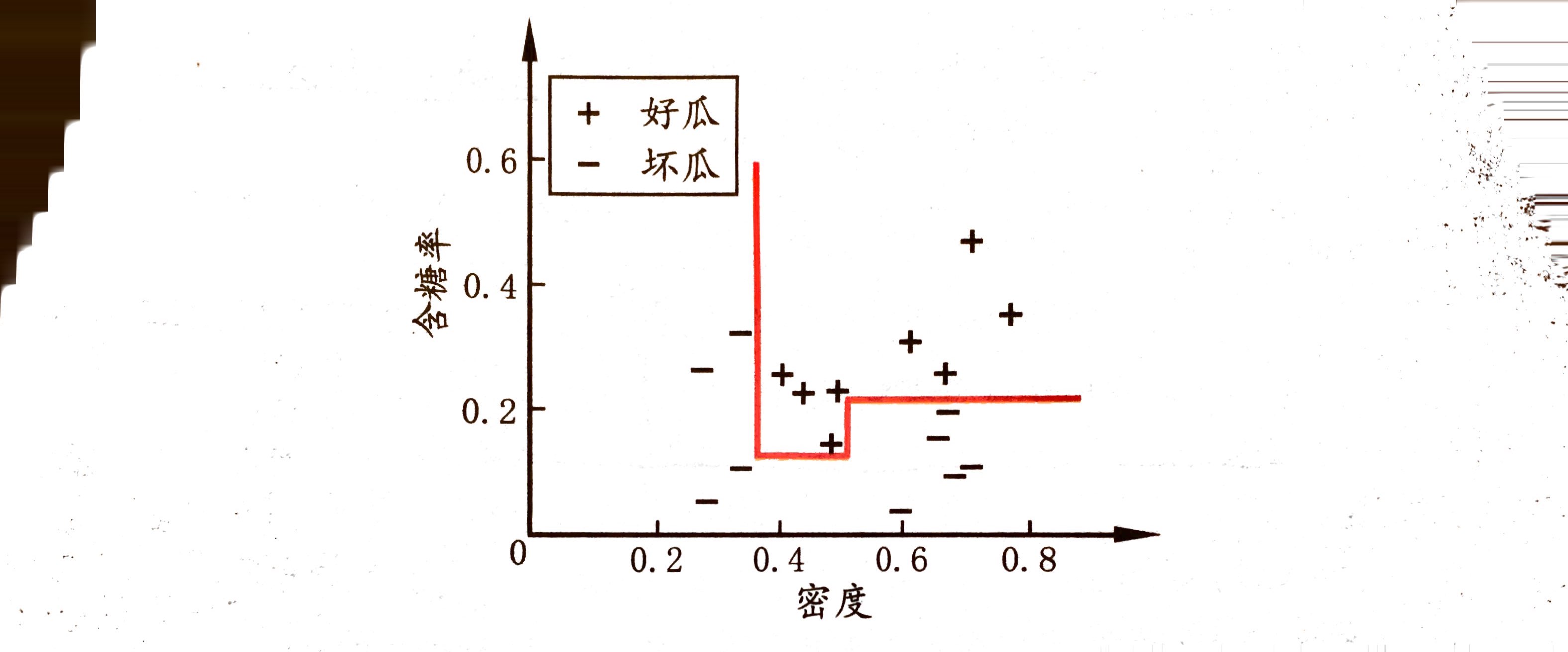
多变量决策树(multivariate decision tree):实现斜划分甚至更复杂划分的决策树。
不是为每个非叶结点寻找一个最优划分属性,而是试图建立一个合适的线性分类器。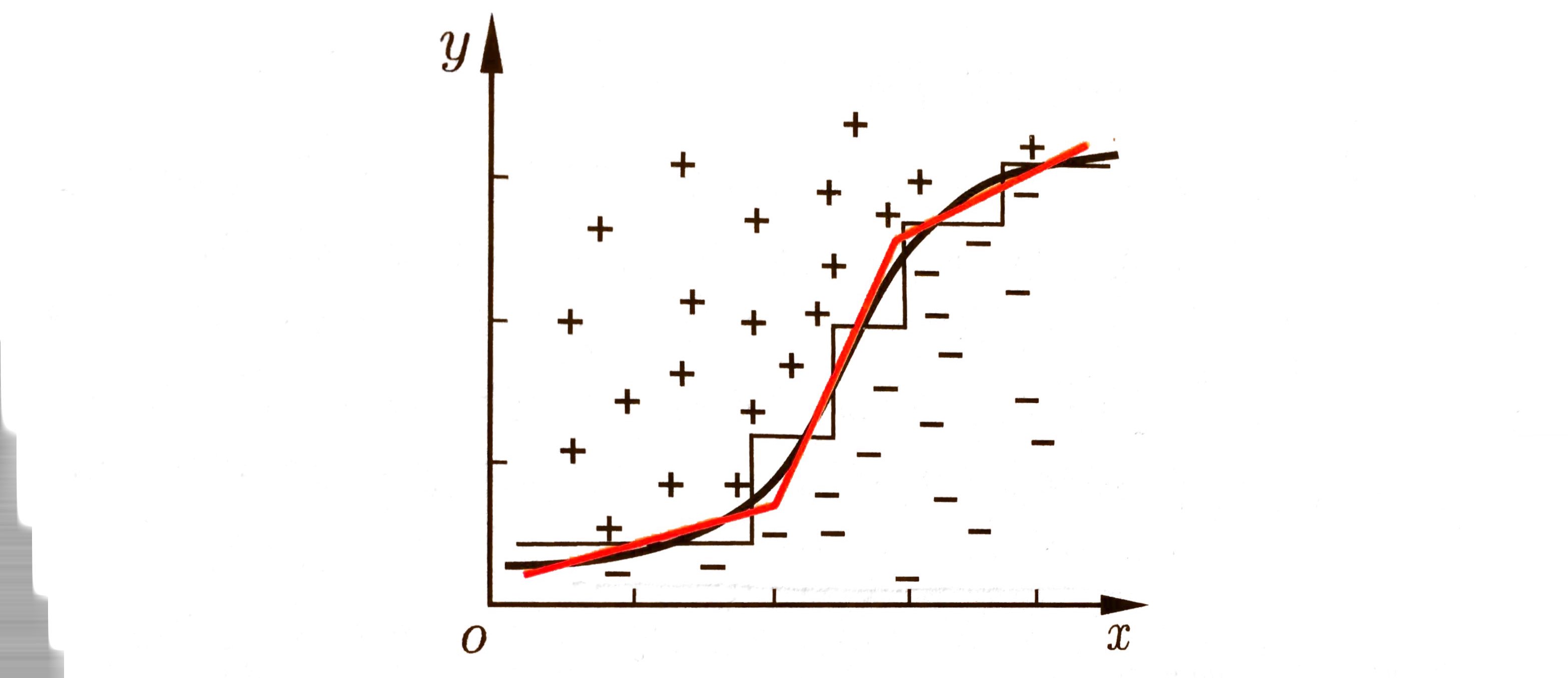
阅读材料
剪枝方法和程度对决策树泛化性能的影响相当显著,最终规则集的泛化性能甚至可能优于原决策树。
有一些决策树学习算法可进行增量学习(incremental learning),接收到新样本后可对已学得的模型进行调整,不用完全重新学习。有效地降低每次接收到新样本后的训练时间开销。