如何实现一个简单的音乐推荐系统
很多人都喜爱听歌,以前我们用 MP3 听歌,现在直接通过音乐 App 在线就能听歌。而且,各种音乐 App 的功能越来越强大,不仅可以自己选歌听,还可以根据你听歌的口味偏好,给你推荐可能会喜爱的音乐,而且有时候,推荐的音乐还非常适合你的口味,甚至会惊艳到你!如此智能的一个功能,你知道它是怎么实现的吗?
算法解析
实际上,要解决这个问题,并不需要特别高深的理论。解决思路的核心思想非常简单、直白,用两句话就能总结出来:
- 找到跟你口味偏好相似的用户,把他们爱听的歌曲推荐给你;
- 找出跟你喜爱的歌曲特征相似的歌曲,把这些歌曲推荐给你;
基于相似用户做推荐
我们把跟你听类似歌曲的人,看作口味相似的用户。你可以看我下面画的这个图。我用“1”表示“喜爱”,用“0”笼统地表示“不发表意见”。从图中我们可以看出,你跟小明共同喜爱的歌曲最多,有 5 首。于是,我们就可以说,小明跟你的口味非常相似: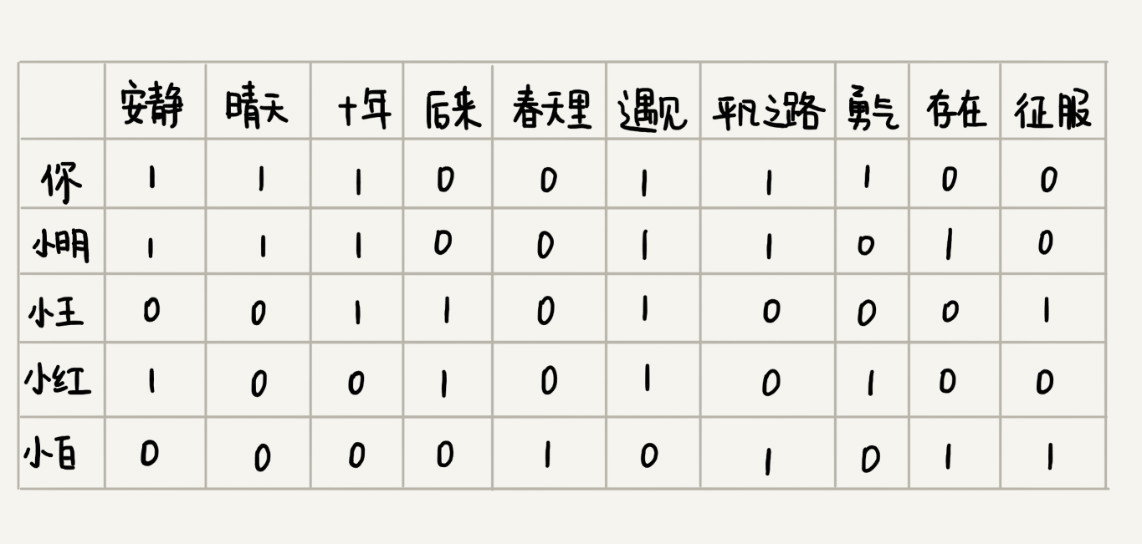
我们只需要遍历所有的用户,对比每个用户跟你共同喜爱的歌曲个数,并且设置一个阈值,如果你和某个用户共同喜爱的歌曲个数超过这个阈值,我们就把这个用户看作跟你口味相似的用户,把这个用户喜爱但你还没听过的歌曲,推荐给你。实际上,我们可以通过用户的行为,来定义这个喜爱程度。我们给每个行为定义一个得分,得分越高表示喜爱程度越高:
我们如果把每个人对每首歌曲的喜爱程度表示出来,就是下面这个样子。图中,某个人对某首歌曲是否喜爱,我们不再用“1”或者“0”来表示,而是对应一个具体的分值: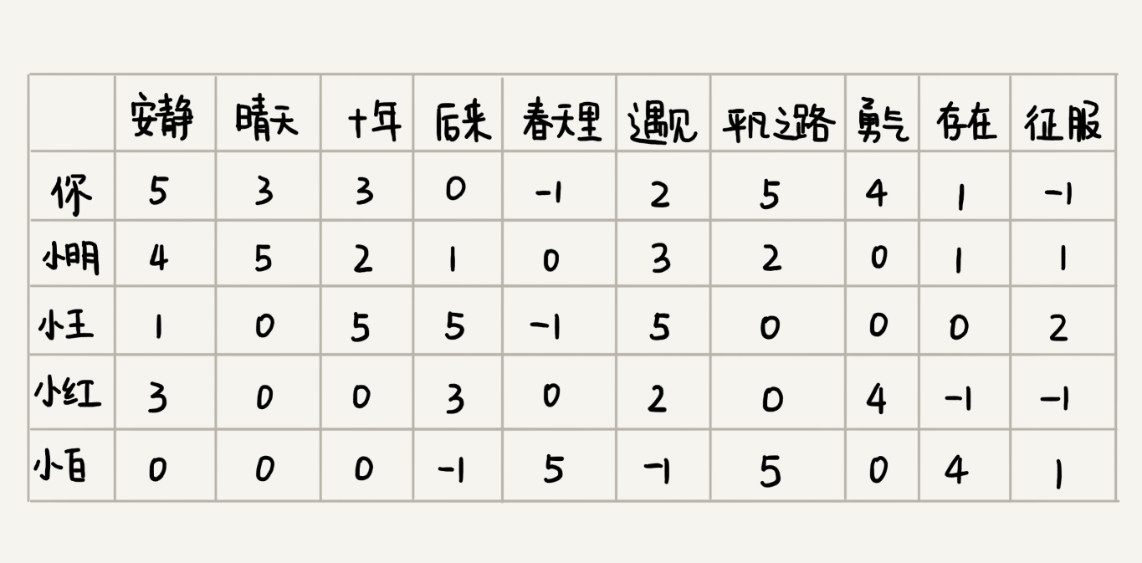
显然,我们不能再像之前那样,采用简单的计数来统计两个用户之间的相似度。这里的相似度度量,我们可以使用另外一个距离,那就是欧几里得距离(Euclidean Distance)。欧几里得距离是用来计算两个向量之间的距离的。一维空间是一条线,我们用 1, 2, 3…这样单个的数,来表示一维空间中的某个位置;二维空间是一个面,我们用 (1, 3), (4, 2), (2, 2)…这样的两个数,来表示二维空间中的某个位置;三维空间是一个立体空间,我们用 (1, 3, 5), (3, 1, 7), (2, 4, 3)…这样的三个数,来表示三维空间中的某个位置。
类比一维, 二维, 三维的表示方法,K 维空间中的某个位置,我们可以写作 (X1, X2, X3, …, XK)。这种表示方法就是向量(Vector)。我们知道,二维, 三维空间中,两个位置之间有距离的概念,类比到高维空间,同样也有距离的概念,这就是我们说的两个向量之间的距离。通过类比,我们就可以得到两个向量之间距离的计算公式。这个计算公式就是欧几里得距离的计算公式:
我们把每个用户对所有歌曲的喜爱程度,都用一个向量表示。我们计算出两个向量之间的欧几里得距离,作为两个用户的口味相似程度的度量。从图中的计算可以看出,小明与你的欧几里得距离距离最小,也就是说,你俩在高维空间中靠得最近,所以,我们就断定,小明跟你的口味最相似: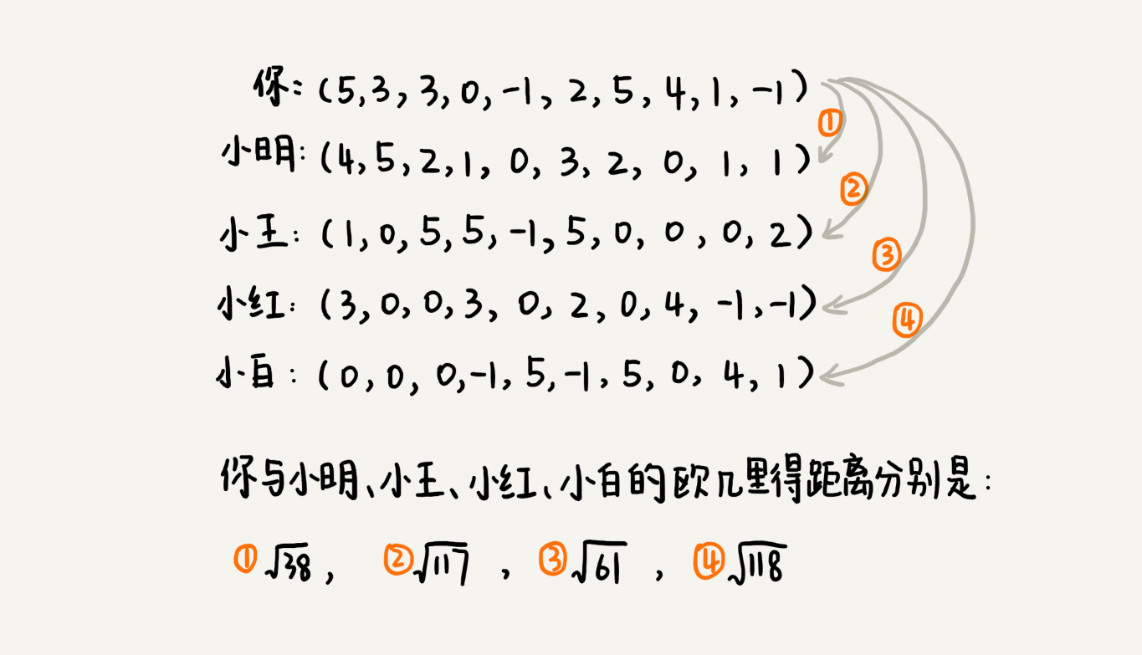
基于相似歌曲做推荐
但是,如果用户是一个新用户,我们还没有收集到足够多的行为数据,这个时候该如何推荐呢?我们现在再来看另外一种推荐方法,基于相似歌曲的推荐方法,也就是说,如果某首歌曲跟你喜爱的歌曲相似,我们就把它推荐给你。基于歌曲特征项计算相似度是不可行的,那我们就换一种思路。对于两首歌,如果喜欢听的人群都是差不多的,那侧面就可以反映出,这两首歌比较相似。如图所示,每个用户对歌曲有不同的喜爱程度,我们依旧通过上一个解决方案中定义得分的标准,来定义喜爱程度:
这个图跟基于相似用户推荐中的图几乎一样。只不过这里把歌曲和用户主次颠倒了一下。基于相似用户的推荐方法中,针对每个用户,我们将对各个歌曲的喜爱程度作为向量;基于相似歌曲的推荐思路中,针对每个歌曲,我们将每个用户的打分作为向量。有了每个歌曲的向量表示,我们通过计算向量之间的欧几里得距离,来表示歌曲之间的相似度。欧几里得距离越小,表示两个歌曲越相似。然后,我们就在用户已经听过的歌曲中,找出他喜爱程度较高的歌曲。然后,我们找出跟这些歌曲相似度很高的其他歌曲,推荐给他。
总结引申
实际上,这个问题是推荐系统(Recommendation System)里最典型的一类问题。之所以讲这部分内容,主要还是想给你展示,算法的强大之处,利用简单的向量空间的欧几里得距离,就能解决如此复杂的问题。不过,今天,我只给你讲解了基本的理论,实践中遇到的问题还有很多,比如冷启动问题,产品初期积累的数据不多,不足以做推荐等等。