C++ STL
在刷题时,我们几乎一定会用到各种数据结构来辅助我们解决问题,因此我们必须熟悉各种数据结构的特点。C++ STL 提供的数据结构包括(实际底层细节可能因编译器而异):
- Sequence Containers:维持顺序的容器:
- vector:动态数组,是我们最常使用的数据结构之一,用于 O(1) 的随机读取。因为大部分算法的时间复杂度都会大于 O(n),因此我们经常新建 vector 来存储各种数据或中间变量。因为在尾部增删的复杂度是 O(1),我们也可以把它当作 stack 来用。
- list:双向链表,也可以当作 stack 和 queue 来使用。由于 LeetCode 的题目多用 Node 来表示链表,且链表不支持快速随机读取,因此我们很少用到这个数据结构(LRU 除外)。
- deque:双端队列,这是一个非常强大的数据结构,既支持 O(1) 随机读取,又支持 O(1) 时间的头部增删和尾部增删(因此可以当作 stack 和 queue 来使用),不过有一定的额外开销。
- array:固定大小的数组,一般在刷题时我们不使用。
- forward_list:单向链表,一般在刷题时我们不使用。
- Container Adaptors:基于其它容器实现的容器:
- stack:后入先出的数据结构,默认基于 deque 实现。stack 常用于深度优先搜索、一些字符串匹配问题以及单调栈问题。
- queue:先入先出的数据结构,默认基于 deque 实现。queue 常用于广度优先搜索。
- priority_queue:最大值先出的数据结构,默认基于 vector 实现堆结构。它可以在 O(nlogn) 的时间排序数组、O(logn) 的时间插入任意值、O(logn) 的时间删除最大值、O(1) 的时间获得最大值。priority_queue 常用于维护数据结构并快速获取最大值,并且可以自定义比较函数,比如通过存储负值或者更改比小函数为比大函数,即可实现最小值先出。
- Ordered Associative Containers:有序关联容器:
- set:有序集合,元素不可重复,底层实现默认为红黑树,即一种特殊的二叉查找树 (BST)。它可以在 O(nlogn) 的时间排序数组,O(logn) 的时间插入、删除、查找任意值,O(logn) 的时间获得最小或最大值。这里注意:set 和 priority_queue 都可以用于维护数据结构并快速获取最大最小值,但是它们的时间复杂度和功能略有区别,如 priority_queue 默认不支持删除任意值,而 set 获得最大或最小值的时间复杂度略高,具体使用哪个根据需求而定。
- multiset:支持重复元素的 set。
- map:有序映射或有序表,在 set 的基础上加上映射关系,可以对每个元素 key 存一个值 value。
- multimap:支持重复元素的 map。
- Unordered Associative Containers:无序关联容器:
- unordered_set:哈希集合,可以在 O(1) 的时间快速插入、查找、删除元素,常用于快速的查询一个元素是否在这个容器内。
- unordered_multiset:支持重复元素的 unordered_set。
- unordered_map:哈希映射或哈希表,在 unordered_set 的基础上加上映射关系,可以对每一个元素 key 存一个值 value。在某些情况下,如果 key 的范围已知且较小,我们也可以用 vector 代替 unordered_map,用位置表示 key,用每个位置的值表示 value。
- unordered_multimap:支持重复元素的 unordered_map。
因为这并不是一本讲解 C++ 原理的书,更多的 STL 细节请读者自行搜索。只有理解了这些数据结构的原理和使用方法,才能够更加游刃有余地解决算法和数据结构问题。
数组
448. Find All Numbers Disappeared in an Array
我们可以直接对原数组进行标记:把重复出现的数字在原数组出现的位置设为负数,最后仍然为正数的位置即为没有出现过的数。
48. Rotate Image
每次只考虑四个间隔 90 度的位置,可以进行 O(1) 额外空间的旋转: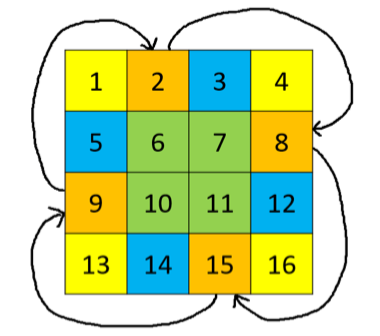
240. Search a 2D Matrix II
这道题有一个简单的技巧:我们可以从右上角开始查找,若当前值大于待搜索值,我们向左移动一位;若当前值小于待搜索值,我们向下移动一位。
769. Max Chunks To Make Sorted
从左往右遍历,同时记录当前的最大值,每当当前最大值等于数组位置时,我们可以多一次分割。
栈和队列
232. Implement Queue using Stacks
我们可以用两个栈来实现一个队列:因为我们需要得到先入先出的结果,所以必定要通过一个额外栈翻转一次数组。这个翻转过程既可以在插入时完成,也可以在取值时完成。
155. Min Stack
我们可以额外建立一个新栈,栈顶表示原栈里所有值的最小值。每当在原栈里插入一个数字时,若该数字小于等于新栈栈顶,则表示这个数字在原栈里是最小值,我们将其同时插入新栈内。每当从原栈里取出一个数字时,若该数字等于新栈栈顶,则表示这个数是原栈里的最小值之一,我们同时取出新栈栈顶的值。
20. Valid Parentheses
括号匹配是典型的使用栈来解决的问题。我们从左往右遍历,每当遇到左括号便放入栈内,遇到右括号则判断其和栈顶的括号是否是统一类型,是则从栈内取出左括号,否则说明字符串不合法。
单调栈
单调栈通过维持栈内值的单调递增(递减)性,在整体 O(n) 的时间内处理需要大小比较的问题。
739. Daily Temperatures
我们可以维持一个单调递减的栈,表示每天的温度;为了方便计算天数差,我们这里存放位置(即日期)而非温度本身。栈内数组永远保持单调递减,避免了使用排序进行比较。
优先队列
优先队列可以在 O(1) 时间内获得最大值,并且可以在 O(logn) 时间内取出最大值或插入任意值。
优先队列常常用堆来实现,堆是一个完全二叉树,其每个节点的值总是大于等于子节点的值。实际实现堆时,我们通常用一个数组而不是用指针建立一个树。这是因为堆是完全二叉树,所以用数组表示时,位置 i 的节点的父节点位置一定为 (i-1)/2,而它的两个子节点的位置又一定分别为 2i+1 和 2i+2。
23. Merge k Sorted Lists
速度比较快的方法:把所有的链表存储在一个优先队列中,每次提取所有链表头部节点值最小的那个节点,直到所有链表都被提取完为止。
218. The Skyline Problem
我们可以使用优先队列储存每个建筑物的高度和右端,从而获取目前会拔高天际线、且妨碍到前一个建筑物(的右端端点)的下一个建筑物。
双端队列
239. Sliding Window Maximum
我们可以利用双端队列进行操作:每当向右移动时,把窗口左端的值从队列左端剔除,把队列右边小于窗口右端的值全部剔除。这样双端队列的最左端永远是当前窗口内的最大值 (单调栈的延申)。
哈希表
哈希表,又称散列表,使用 O(n) 空间复杂度存储数据,通过哈希函数映射位置,从而实现近似 O(1) 时间复杂度的插入、查找、删除等操作。
C++ 中的哈希集合为 unordered_set,可以查找元素是否在集合中。如果需要同时存储键和值,则需要用 unordered_map,可以用来统计频率,记录内容等等。如果元素有穷,并且范围不大,那么可以用一个固定大小的数组来存储或统计元素。
1. Two Sum
我们可以利用哈希表存储遍历过的值以及它们的位置,每次遍历到位置 i 的时候,查找哈希表里是否存在 target-nums[i],若存在,则说明这两个值的和为 target。
128. Longest Consecutive Sequence
我们可以把所有数字放到一个哈希表,然后不断地从哈希表中任意取一个值,并删除掉其之前之后的所有连续数字,然后更新目前的最长连续序列长度。
149. Max Points on a Line
对于每个点,我们对其它点建立哈希表,统计同一斜率的点一共有多少个。这里利用的原理是,一条线可以由一个点和斜率而唯一确定。另外也要考虑斜率不存在和重复坐标的情况。
多重集合和映射
332. Reconstruct Itinerary
本题可以先用哈希表记录起止机场,其中键是起始机场,值是一个多重(有序)集合,表示对应的终止机场。储存完成之后,我们可以利用栈来恢复从终点到起点飞行的顺序,再将结果逆序得到从起点到终点的顺序。
前缀和与积分图
一维的前缀和 (Cumulative Sum)、二维的积分图 (Image Integral),都是把每个位置之前的一维线段或二维矩形预先存储,方便加速计算:
- 如果需要对前缀和或积分图的值做寻址,则要存入哈希表。
- 如果要对每个位置记录前缀和或积分图的值,则可以存储到一维或二维数组里,也常常伴随着动态规划。
303. Range Sum Query - Immutable
对于一维的数组,我们可以使用前缀和来解决此类问题。先建立一个与数组 nums 长度相同的新数组 psum,表示 nums 每个位置之前所有数字的和。如果我们需要获得位置 i 和 j 之间的数字和,只需计算 psum[j+1] - psum[i] 即可。
304. Range Sum Query 2D - Immutable
类似于前缀和,我们可以把这种思想拓展到二维,即积分图。我们可以先建立一个 dp 矩阵,dp[i][j] 表示以位置 (0, 0) 为左上角、位置 (i-1, j-1) 为右下角的长方形中所有数字的和。
我们可以用动态规划来计算 dp 矩阵:dp[i][j] = matrix[i-1][j-1] + dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1],即当前坐标的数字 + 上面长方形的数字和 + 左边长方形的数字和 - 上面长方形和左边长方形重合面积(即左上一格的长方形)中的数字和: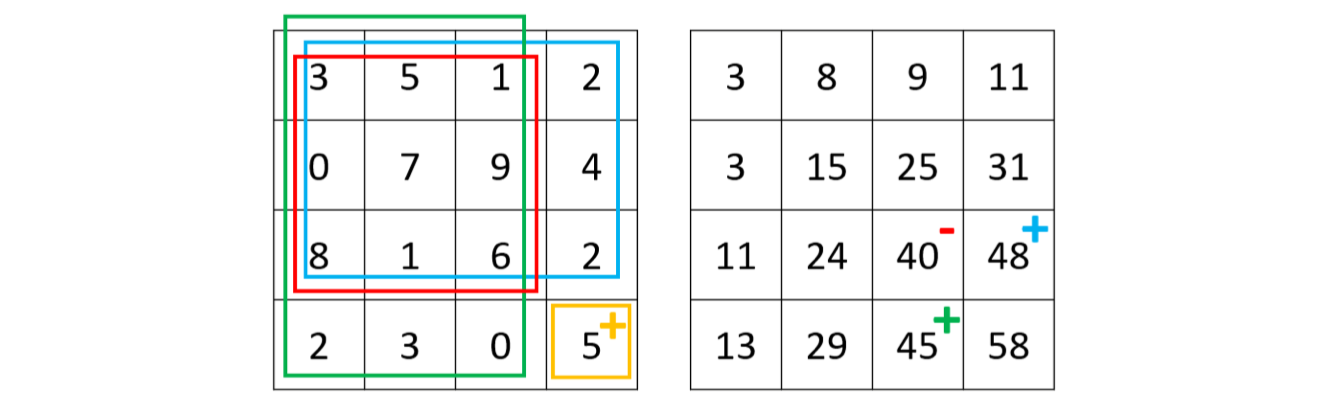
假设我们要查询长方形 E 的数字和,因为 E = D − B − C + A,我们发现 E 其实可以由四个位置的积分图结果进行加减运算得到。因此这个算法在预处理时的时间复杂度为 O(mn),而在查询时的时间复杂度仅为 O(1):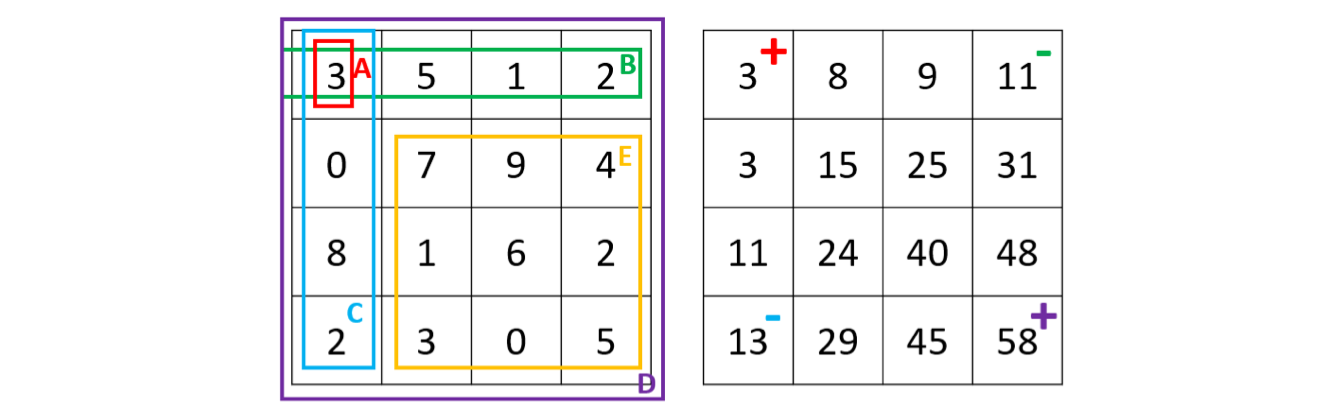
560. Subarray Sum Equals K
本题同样是利用前缀和,不同的是这里我们使用一个哈希表 freq,其键是前缀和,而值是该前缀和出现的次数。在我们遍历到位置 i 时,假设当前的前缀和是 psum,那么 freq[psum-k] 即为以当前位置结尾、满足条件的区间个数。
练习
566. Reshape the Matrix
没有什么难度,只是需要一点耐心。
225. Implement Stack using Queues
利用相似的方法,我们也可以用 stack 实现 queue。
503. Next Greater Element II
Daily Temperature 的变种题。
217. Contains Duplicate
使用什么数据结构可以快速判断重复呢?
697. Degree of an Array
如何对数组进行预处理才能正确并快速地计算子数组的长度?
594. Longest Harmonious Subsequence
最长连续序列的变种题。
15. 3Sum
因为排序的复杂度是 O(nlogn) < O(n^2),因此我们既可以排序后再进行 O(n^2) 的指针搜索,也可以直接利用哈希表进行 O(n^2) 的搜索。
287. Find the Duplicate Number
寻找丢失数字的变种题。除了标负位置,你还有没有其它算法可以解决这个问题?
313. Super Ugly Number
尝试使用优先队列解决这一问题。
870. Advantage Shuffle
如果我们需要比较大小关系,而且同一数字可能出现多次,那么应该用什么数据结构呢?
307. Range Sum Query - Mutable
前缀和的变种题。好吧我承认,这道题可能有些超纲,你或许需要搜索一下什么是线段树。