最短路径

Posted on

地图软件是如何计算出最优出行路径的

像 Google 地图、百度地图、高德地图这样的地图软件，我想你应该经常使用吧？如果想从家开车到公司，你只需要输入起始、结束地址，地图就会给你规划一条最优出行路线。这里的最优，有很多种定义，比如最短路线、最少用时路线、最少红绿灯路线等等。作为一名软件开发工程师，你是否思考过，地图软件的最优路线是如何计算出来的吗？底层依赖了什么算法呢？

算法解析

解决软件开发中的实际问题，最重要的一点就是建模，也就是将复杂的场景抽象成具体的数据结构。我们把每个岔路口看作一个顶点，岔路口与岔路口之间的路看作一条边，路的长度就是边的权重。如果路是单行道，我们就在两个顶点之间画一条有向边；如果路是双行道，我们就在两个顶点之间画两条方向不同的边。这样，整个地图就被抽象成一个有向有权图。于是，我们要求解的问题就转化为，在一个有向有权图中，求两个顶点间的最短路径：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
public class Graph 
{ 
    // 有向有权图的邻接表表示
    private LinkedList<Edge> adj[]; // 邻接表
    private int v; // 顶点个数

    public Graph(int v) 
    {
        this.v = v;
        this.adj = new LinkedList[v];
        for (int i = 0; i < v; ++i) 
        {
            this.adj[i] = new LinkedList<>();
        }
    }

    public void addEdge(int s, int t, int w) 
    { 
        // 添加一条边
        this.adj[s].add(new Edge(s, t, w));
    }

    private class Edge 
    {
        public int sid; // 边的起始顶点编号
        public int tid; // 边的终止顶点编号
        public int w;   // 权重
        public Edge(int sid, int tid, int w) 
        {
            this.sid = sid;
            this.tid = tid;
            this.w = w;
        }
    }
    // 下面这个类是为了 Dijkstra 实现用的
    private class Vertex 
    {
        public int id;   // 顶点编号 ID
        public int dist; // 从起始顶点到这个顶点的距离
        public Vertex(int id, int dist) 
        {
            this.id = id;
            this.dist = dist;
        }
    }
}

想要解决这个问题，有一个非常经典的算法，最短路径算法（Shortest Path Algorithm），更加准确地说，是单源最短路径算法（一个顶点到一个顶点）。提到最短路径算法，最出名的莫过于 Dijkstra 算法了。所以，我们现在来看，Dijkstra 算法是怎么工作的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
// 因为 Java 提供的优先级队列，没有暴露更新数据的接口，所以我们需要重新实现一个
private class PriorityQueue 
{ 
    // 根据 vertex.dist 构建小顶堆
    private Vertex[] nodes;
    private int count;
    public PriorityQueue(int v) 
    {
        this.nodes = new Vertex[v+1];
        this.count = v;
    }
    public Vertex poll() 
    { 
        // TODO: ...
    }
    public void add(Vertex vertex) 
    { 
        // TODO: ...
    }
    // 更新结点的值，并且从下往上堆化，重新符合堆的定义；时间复杂度 O(logn)
    public void update(Vertex vertex) 
    { 
        // TODO: ...
    } 
    public boolean isEmpty() 
    { 
        // TODO: ...
    }
}

public void dijkstra(int s, int t) 
{ 
    // 从顶点 s 到顶点 t 的最短路径
    int[] predecessor = new int[this.v]; // 用来还原最短路径
    Vertex[] vertexes = new Vertex[this.v];
    for (int i = 0; i < this.v; ++i) 
    {
        vertexes[i] = new Vertex(i, Integer.MAX_VALUE);
    }
    PriorityQueue queue = new PriorityQueue(this.v); // 小顶堆
    boolean[] inqueue = new boolean[this.v]; // 标记是否进入过队列
    vertexes[s].dist = 0;
    queue.add(vertexes[s]);
    inqueue[s] = true;
    while (!queue.isEmpty()) 
    {
        Vertex minVertex= queue.poll(); // 取堆顶元素并删除
        if (minVertex.id == t)
        {
            break; // 最短路径产生了
        }
        for (int i = 0; i < adj[minVertex.id].size(); ++i) 
        {
            Edge e = adj[minVertex.id].get(i);   // 取出一条 minVertex 相连的边
            Vertex nextVertex = vertexes[e.tid]; // minVertex->nextVertex
            if (minVertex.dist + e.w < nextVertex.dist) 
            { 
                // 更新 next 的 dist
                nextVertex.dist = minVertex.dist + e.w;
                predecessor[nextVertex.id] = minVertex.id;
                if (inqueue[nextVertex.id] == true) 
                {
                    queue.update(nextVertex); // 更新队列中的 dist 值
                } 
                else 
                {
                    queue.add(nextVertex);
                    inqueue[nextVertex.id] = true;
                }
            }
        }
    }
    // 输出最短路径
    System.out.print(s);
    print(s, t, predecessor);
}

private void print(int s, int t, int[] predecessor) 
{
    if (s == t)
    {
        return;
    }
    print(s, predecessor[t], predecessor);
    System.out.print("->" + t);
}

我们用 vertexes 数组，记录从起始顶点到每个顶点的距离（dist）。起初，我们把所有顶点的 dist 都初始化为无穷大，把起始顶点的 dist 值初始化为 0，然后将其放到优先级队列中。

我们从优先级队列中取出 dist 最小的顶点 minVertex，然后考察这个顶点可达的所有顶点（代码中的 nextVertex）。如果 minVertex 的 dist 值加上 minVertex 与 nextVertex 之间边的权重 w 小于 nextVertex 当前的 dist 值，也就是说，存在另一条更短的路径，它经过 minVertex 到达 nextVertex。那我们就把 nextVertex 的 dist 更新为 minVertex 的 dist 值加上 w。然后，我们把 nextVertex 加入到优先级队列中。重复这个过程，直到找到终止顶点 t 或者队列为空。

predecessor 数组的作用是为了还原最短路径，它记录每个顶点的前驱顶点。最后，我们通过递归的方式，将这个路径打印出来；inqueue 数组是为了避免将一个顶点多次添加到优先级队列中。我们更新了某个顶点的 dist 值之后，如果这个顶点已经在优先级队列中了，就不要再将它重复添加进去了。我举个例子，再给你解释一下：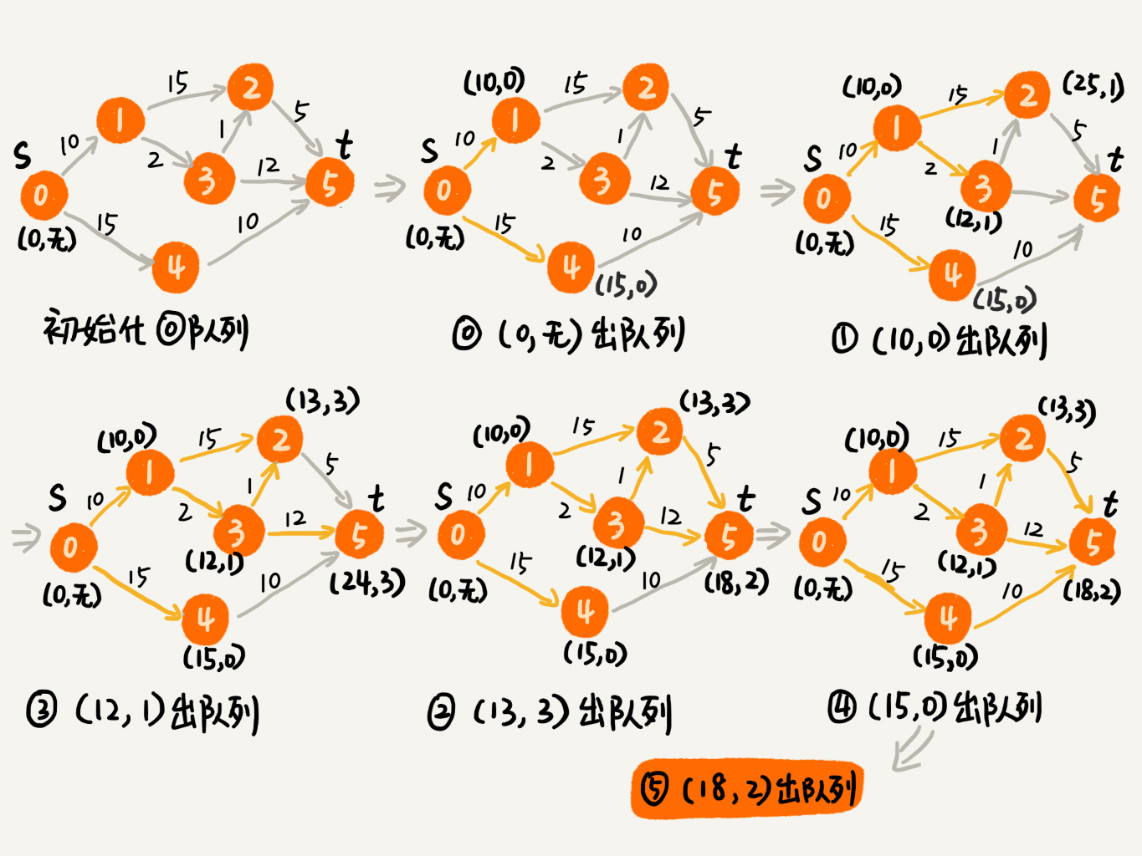

在刚刚的代码实现中，最复杂就是 while 循环嵌套 for 循环那部分代码了。while 循环最多会执行 V 次，而内部的 for 循环的执行次数不确定，跟每个顶点的相邻边的个数有关，我们分别记作 E0, E1, E2, …, E(V-1)。如果我们把这 V 个顶点的边都加起来，最大也不会超过图中所有边的个数 E。

for 循环内部的代码涉及从优先级队列取数据、往优先级队列中添加数据、更新优先级队列中的数据，这样三个主要的操作。我们知道，优先级队列是用堆来实现的，堆中的这几个操作，时间复杂度都是 O(logV)。所以，综合这两部分，再利用乘法原则，整个代码的时间复杂度就是 O(E*logV)。

前面讲最短路径的时候，每条边的权重是路的长度。在计算最少时间的时候，算法还是不变，我们只需要把边的权重，从路的长度变成经过这段路所需要的时间。不过，这个时间会根据拥堵情况时刻变化。

每经过一条边，就要经过一个红绿灯。关于最少红绿灯的出行方案，实际上，我们只需要把每条边的权值改为 1 即可，算法还是不变，可以继续使用前面讲的 Dijkstra 算法。不过，边的权值为 1，也就相当于无权图了，我们还可以使用之前讲过的广度优先搜索算法。因为我们前面讲过，广度优先搜索算法计算出来的两点之间的路径，就是两点的最短路径。

总结引申

我们有一个翻译系统，只能针对单个词来做翻译。如果要翻译一整个句子，我们需要将句子拆成一个一个的单词，再丢给翻译系统。针对每个单词，翻译系统会返回一组可选的翻译列表，并且针对每个翻译打一个分，表示这个翻译的可信程度：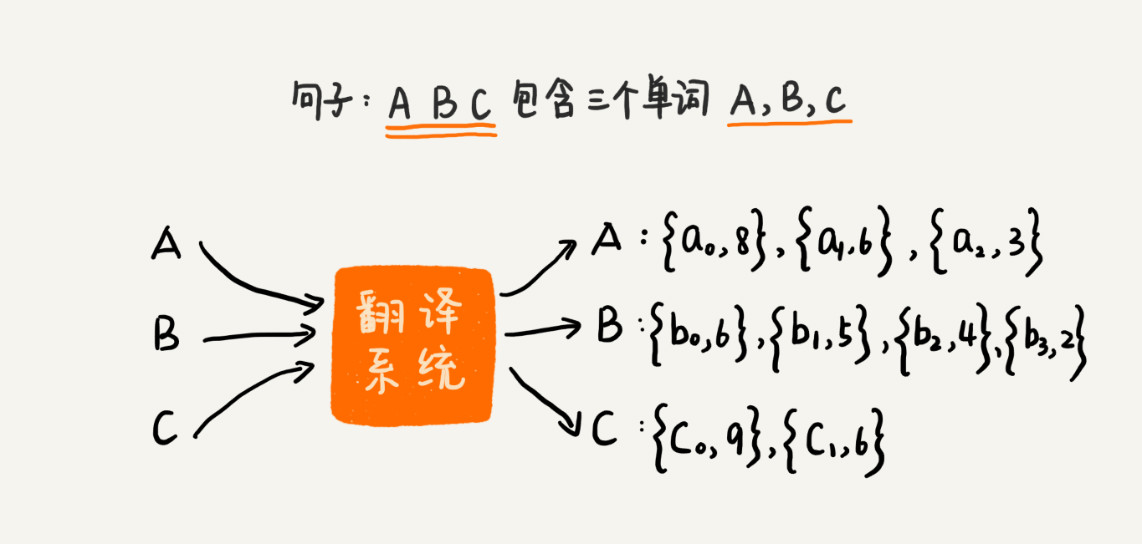

针对每个单词，我们从可选列表中，选择其中一个翻译，组合起来就是整个句子的翻译。每个单词的翻译的得分之和，就是整个句子的翻译得分。随意搭配单词的翻译，会得到一个句子的不同翻译。针对整个句子，我们希望计算出得分最高的前 k 个翻译结果：

当然，最简单的办法还是借助回溯算法，穷举所有的排列组合情况，然后选出得分最高的前 k 个翻译结果。但是，这样做的时间复杂度会比较高，是 O(m^n)，其中，m 表示平均每个单词的可选翻译个数，n 表示一个句子中包含多少个单词。实际上，这个问题可以借助 Dijkstra 算法的核心思想，非常高效地解决。每个单词的可选翻译是按照分数从大到小排列的，所以 a0​b0​c0​ 肯定是得分最高组合结果。我们把 a0​b0​c0​ 及得分作为一个对象，放入到优先级队列中。

我们每次从优先级队列中取出一个得分最高的组合，并基于这个组合进行扩展。扩展的策略是每个单词的翻译分别替换成下一个单词的翻译。比如 a0​b0​c0​ 扩展后，会得到三个组合：a1​b0​c0​, a0​b1​c0​, a0​b0​c1​。我们把扩展之后的组合，加到优先级队列中。重复这个过程，直到获取到 k 个翻译组合或者队列为空：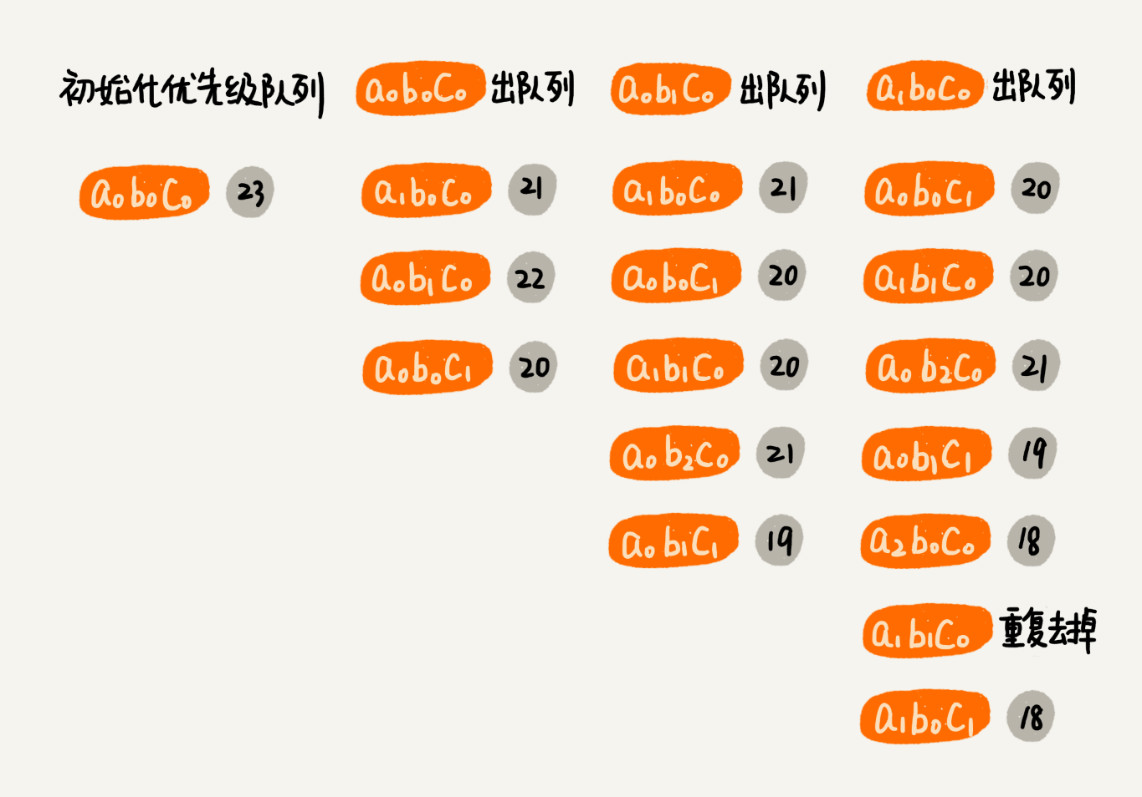

假设句子包含 n 个单词，每个单词平均有 m 个可选的翻译，我们求得分最高的前 k 个组合结果。每次一个组合出队列，就对应着一个组合结果，我们希望得到 k 个，那就对应着 k 次出队操作。每次有一个组合出队列，就有 n 个组合入队列。优先级队列中出队和入队操作的时间复杂度都是 O(logX)，X 表示队列中的组合个数。所以，总的时间复杂度就是 O(k*n*logX)。

k 次出入队列，队列中的总数据不会超过 k*n，也就是说，出队、入队操作的时间复杂度是 O(log(k*n))。所以，总的时间复杂度就是 O(k*n*log(k*n))，比之前的指数级时间复杂度降低了很多。