Sliding Window

Posted on

难点大概是 shrink 的时机。窗口大小固定时，借助 end - start + 1；不固定时，借助基于 matched 的 while 循环。

In many problems dealing with an array (or a linked list), we are asked to find or calculate something among all the contiguous subarrays (or sublists) of a given size. For example, take a look at this problem:

Given an array, find the average of all contiguous subarrays of size “K” in it.

Let’s understand this problem with a real input:

1
Array: [1, 3, 2, 6, -1, 4, 1, 8, 2], K=5

Here, we are asked to find the average of all contiguous subarrays of size “5” in the given array. Let’s solve this:

  1. For the first 5 numbers (subarray from index 0~4), the average is: (1+3+2+6-1)/5 = 2.2;
  2. The average of next 5 numbers (subarray from index 1~5) is: (3+2+6-1+4)/5 = 2.8;
  3. For the next 5 numbers (subarray from index 2~6), the average is: (2+6-1+4+1)/5 = 2.4;
  4. …

Here is the final output containing the averages of all contiguous subarrays of size 5:

1
Output: [2.2, 2.8, 2.4, 3.6, 2.8]

A brute-force algorithm will calculate the sum of every 5-element contiguous subarray of the given array and divide the sum by “5” to find the average. This is what the algorithm will look like:

1
2
3
4
5
6
7
8
9
10
11
def find_average_of_subarrays(k, arr):
    ans = []
    for i in range(len(arr) - k + 1):
        # find sum of next k elements
        element_sum = 0
        for j in range(i, i + k):
            element_sum += arr[j]
        
        ans.append(element_sum / k)

    return ans

Time Complexity: Since for every element of the input array, we are calculating the sum of its next “K” elements, the time complexity of the above algorithm will be O(N*K) where “N” is the number of elements in the input array.

The inefficiency is that for any two consecutive subarrays of size “5”, the overlapping part (which will contain four elements) will be evaluated twice. For example, take the above-mentioned input:

As you can see, there are four overlapping elements between the subarray (indexed from 0~4) and the subarray (indexed from 1~5). Can we somehow reuse the sum we have calculated for the overlapping elements?

The efficient way to solve this problem would be to visualize each contiguous subarray as a sliding window of “5” elements. This means that we will slide the window by one element when we move on to the next subarray. To reuse the sum from the previous subarray, we will subtract the element going out of the window and add the element now being included in the sliding window. This will save us from going through the whole subarray to find the sum and, as a result, the algorithm complexity will reduce to O(N):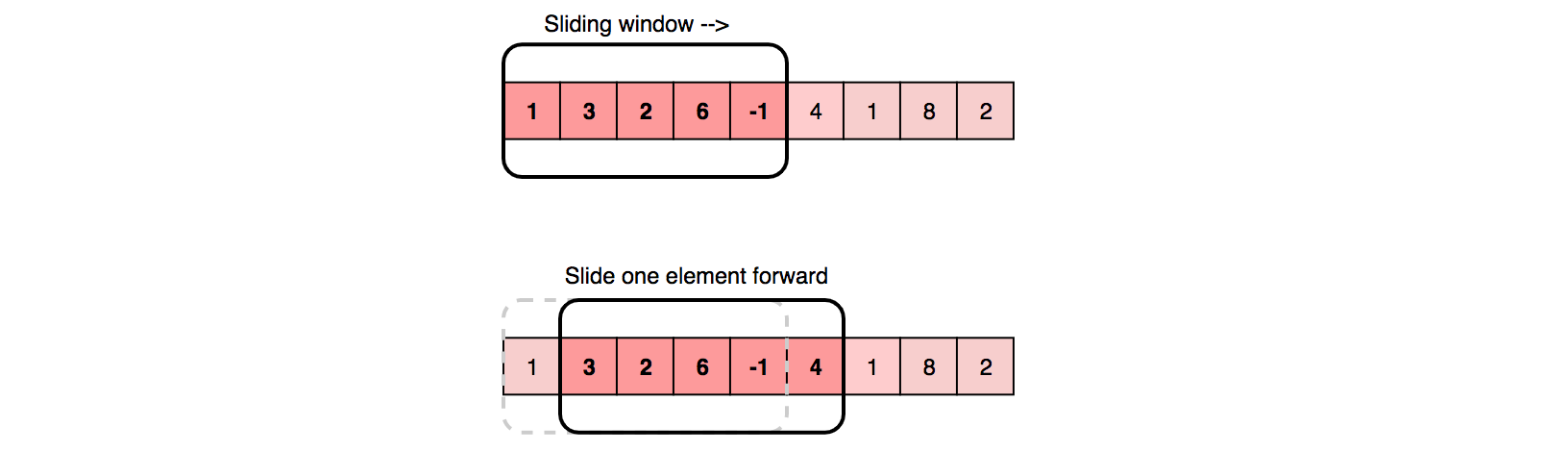

Here is the algorithm for the Sliding Window approach:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def find_average_of_subarrays(k, arr):
    ans = []
    window_sum = 0

    start = 0
    for end in range(len(arr)):
        window_sum += arr[end]
        
        # shrink
        if end >= k - 1:
            ans.append(window_sum / k)
            window_sum -= arr[start]
            start += 1
    
    return ans

In some problems, the size of the sliding window is not fixed. We have to expand or shrink the window based on the problem constraints.

Snippets

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
freq = dict()
for char in t:
    freq[char] = freq.get(char, 0) + 1

matched = 0
ans = ""

start = 0
for end in range(len(s)):
    if s[end] in freq:
        freq[s[end]] -= 1
        if freq[s[end]] == 0:
            matched += 1

    # shrink
    while matched == len(freq):
        if not ans or end - start + 1 < len(ans):
            ans = s[start:end+1]

        if s[start] in freq:
            if freq[s[start]] == 0:
                matched -= 1
            freq[s[start]] += 1

        start += 1

return ans

LeetCode

53. Maximum Subarray
209. Minimum Size Subarray Sum
340. Longest Substring with At Most K Distinct Characters
904. Fruit Into Baskets
3. Longest Substring Without Repeating Characters
424. Longest Repeating Character Replacement
1004. Max Consecutive Ones III
567. Permutation in String
438. Find All Anagrams in a String
76. Minimum Window Substring
30. Substring with Concatenation of All Words