数据结构介绍
作为指针三剑客之三,图是树的升级版。图通常分为有向 (Directed) 或无向 (Undirected),有循环 (Cyclic) 或无循环 (Acyclic),所有节点相连 (Connected) 或不相连 (Disconnected)。树即是一个相连的无向无环图,而另一种很常见的图是有向无环图 (DAG):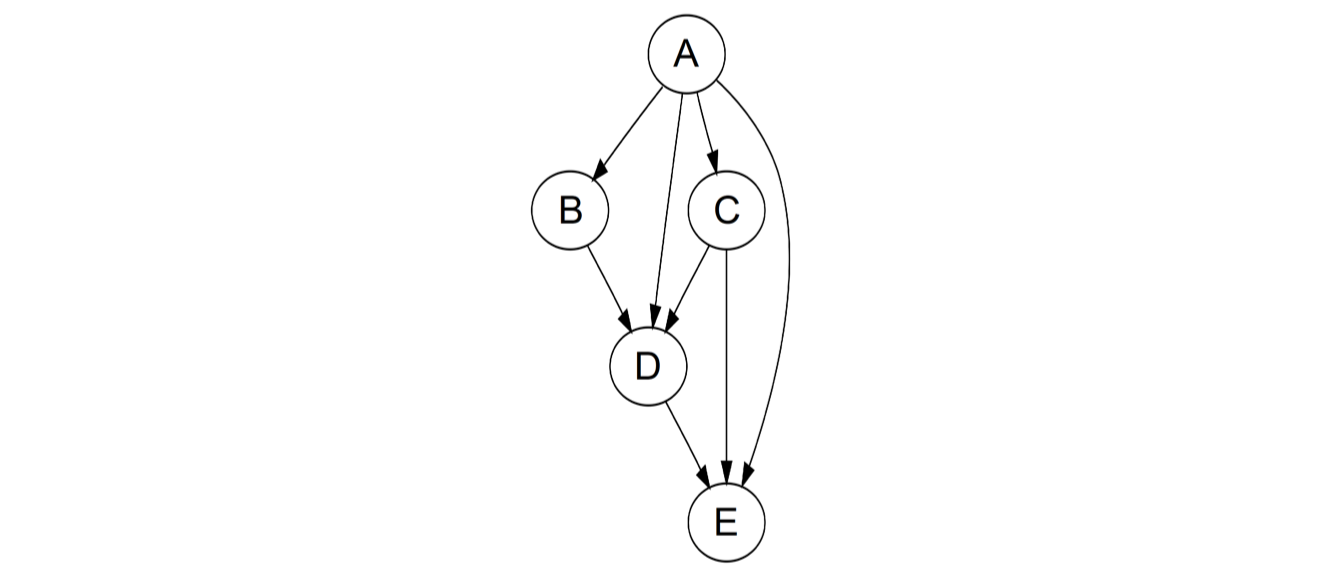
假设图中一共有 n 个节点、m 条边,图通常有两种表示方法:
- 邻接矩阵 (Adjacency Matrix):我们可以建立一个 n×n 的矩阵 G,如果第 i 个节点连向第 j 个节点,则 G[i][j]=1,反之为 0;如果图是无向的,则这个矩阵一定是对称矩阵,即 G[i][j]=G[j][i];
- 邻接链表 (Adjacency List):我们可以建立一个大小为 n 的数组,每个位置 i 储存一个数组或者链表,表示第 i 个节点连向的其它节点;
邻接矩阵空间开销比邻接链表大,但是邻接链表不支持快速查找 i 和 j 是否相连,因此两种表示方法可以根据题目需要适当选择。除此之外,我们也可以直接用一个 m×2 的矩阵储存所有的边。
二分图
二分图算法也称为染色法,是一种广度优先搜索。如果可以用两种颜色对图中的节点进行着色,并且保证相邻的节点颜色不同,那么图为二分。
785. Is Graph Bipartite?
利用队列和广度优先搜索,我们可以对未染色的节点进行染色,并且检查是否有颜色相同的相邻节点存在。
拓扑排序
拓扑排序 (Topological Sort) 是一种常见的,对有向无环图排序的算法。给定有向无环图中的 N 个节点,我们把它们排序成一个线性序列;若原图中节点 i 指向节点 j,则排序结果中 i 一定在 j 之前。拓扑排序的结果不是唯一的,只要满足以上条件即可。
210. Course Schedule II
拓扑排序也可以被看成是广度优先搜索的一种情况:我们先遍历一遍所有节点,把入度为 0 的节点(即没有前置课程要求)放在队列中。在每次从队列中获得节点时,我们将该节点放在目前排序的末尾,并且把它指向的课程的入度各减 1;如果在这个过程中有课程的所有前置必修课都已修完(即入度为 0),我们把这个节点加入队列中。
练习
1059. All Paths from Source Lead to Destination
虽然使用深度优先搜索可以解决大部分的图遍历问题,但是注意判断是否陷入了环路。
1135. Connecting Cities With Minimum Cost
本题考察最小生成树 (MST) 的求法,通常可以用两种方式求得:Prim’s Algorithm,利用优先队列选择最小的消耗;以及 Kruskal’s Algorithm,排序后使用并查集。
882. Reachable Nodes In Subdivided Graph
本题是经典的节点最短距离问题,常用的算法有 Bellman-Ford 单源最短路算法,以及 Dijkstra 无负边单源最短路算法。虽然经典,但是 LeetCode 很少有相关的题型,因此这里仅供读者自行深入学习。