回溯算法

Posted on

如何理解“回溯算法”？

笼统地讲，回溯算法（Backtracking Algorithm）很多时候都应用在“搜索”这类问题上。不过这里说的搜索，并不是狭义的指我们前面讲过的图的搜索算法，而是在一组可能的解中，搜索满足期望的解。回溯的处理思想，有点类似枚举搜索。我们枚举所有的解，找到满足期望的解。为了有规律地枚举所有可能的解，避免遗漏和重复，我们把问题求解的过程分为多个阶段。每个阶段，我们都会面对一个岔路口，我们先随意选一条路走，当发现这条路走不通的时候（不符合期望的解），就回退到上一个岔路口，另选一种走法继续走。

我们有一个 8x8 的棋盘，希望往里放 8 个棋子（皇后），每个棋子所在的行、列、对角线都不能有另一个棋子。你可以看我画的图，第一幅图是满足条件的一种方法，第二幅图是不满足条件的。八皇后问题就是期望找到所有满足这种要求的放棋子方式：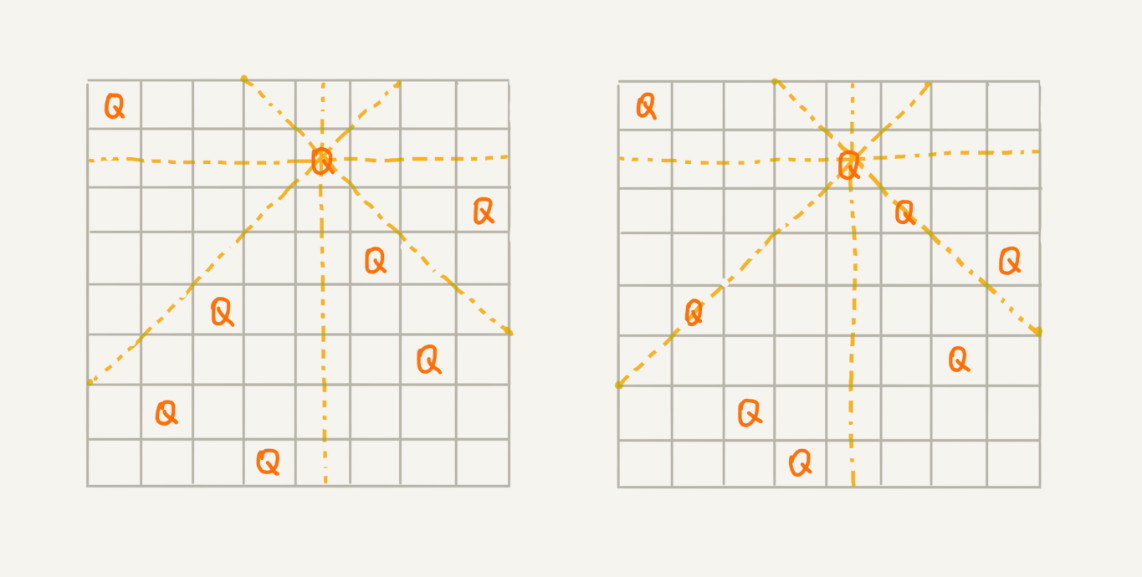

我们把这个问题划分成 8 个阶段，依次将 8 个棋子放到第一行, 第二行, 第三行, …, 第八行。在放置的过程中，我们不停地检查当前放法，是否满足要求。如果满足，则跳到下一行继续放置棋子；如果不满足，那就再换一种放法，继续尝试。回溯算法非常适合用递归代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
int[] result = new int[8]; // 全局或成员变量，下标表示行，值表示 queen 存储在哪一列
public void cal8queens(int row) 
{ 
    // 调用方式：cal8queens(0);
    if (row == 8) 
    { 
        // 8 个棋子都放置好了，打印结果
        printQueens(result);
        return; // 8 行棋子都放好了，已经没法再往下递归了，所以就 return
    }
    for (int column = 0; column < 8; ++column) 
    { 
        // 每一行都有 8 种放法
        if (isOk(row, column)) 
        { 
            // 有些放法不满足要求
            result[row] = column; // 第 row 行的棋子放到了 column 列
            cal8queens(row+1);    // 考察下一行
        }
    }
}

private boolean isOk(int row, int column) 
{
    // 判断 row 行 column 列放置是否合适
    int leftup = column - 1, rightup = column + 1;
    for (int i = row-1; i >= 0; --i) 
    { 
        // 逐行往上考察每一行
        if (result[i] == column)
        {
            return false; // 第 i 行的 column 列有棋子吗
        }
        if (leftup >= 0) 
        { 
            // 考察左上对角线：第 i 行 leftup 列有棋子吗
            if (result[i] == leftup) 
            {
                return false;
            }
        }
        if (rightup < 8) 
        { 
            // 考察右上对角线：第 i 行 rightup 列有棋子吗
            if (result[i] == rightup)
            {
                return false;
            }
        }
        --leftup; ++rightup;
    }
    return true;
}

private void printQueens(int[] result) 
{ 
    // 打印出一个二维矩阵
    for (int row = 0; row < 8; ++row) 
    {
        for (int column = 0; column < 8; ++column) 
        {
            if (result[row] == column) 
            {
                System.out.print("Q ");
            }
            else
            {
                System.out.print("* ");
            }
        }
        System.out.println();
    }
    System.out.println();
}

两个回溯算法的经典应用

回溯算法的理论知识很容易弄懂。不过，对于新手来说，比较难的是用递归来实现。

0-1 背包

0-1 背包是非常经典的算法问题，很多场景都可以抽象成这个问题模型。这个问题的经典解法是动态规划，不过还有一种简单但没有那么高效的解法，那就是回溯算法。0-1 背包问题有很多变体，我这里介绍一种比较基础的。我们有一个背包，背包总的承载重量是 Wkg。现在我们有 n 个物品，每个物品的重量不等，并且不可分割。我们现在期望选择几件物品，装载到背包中。在不超过背包所能装载重量的前提下，如何让背包中物品的总重量最大。由于物品是不可分割的，要么装要么不装，所以叫 0-1 背包问题。

对于每个物品来说，都有两种选择，装进背包或者不装进背包。对于 n 个物品来说，总的装法就有 2^n 种，去掉总重量超过 Wkg 的，从剩下的装法中选择总重量最接近 Wkg 的。这里就可以用回溯的方法。我们可以把物品依次排列，整个问题就分解为了 n 个阶段，每个阶段对应一个物品怎么选择。先对第一个物品进行处理，选择装进去或者不装进去，然后再递归地处理剩下的物品。这里还稍微用到了一点搜索剪枝的技巧，就是当发现已经选择的物品的重量超过 Wkg 之后，我们就停止继续探测剩下的物品：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public int maxW = Integer.MIN_VALUE; // 存储背包中物品总重量的最大值
// cw 表示当前已经装进去的物品的重量和；i 表示考察到哪个物品了
// w 背包重量；items 表示每个物品的重量；n 表示物品个数
// 假设背包可承受重量 100，物品个数 10，物品重量存储在数组 a 中，那可以这样调用函数：
// f(0, 0, a, 10, 100)
public void f(int i, int cw, int[] items, int n, int w) 
{
    if (cw == w || i == n) 
    { 
        // cw==w 表示装满了；i==n 表示已经考察完所有的物品
        if (cw > maxW)
        { 
            maxW = cw;
        }
        return;
    }
    f(i+1, cw, items, n, w); // 当前物品不装进背包
    if (cw + items[i] <= w) 
    {
        // 已经超过可以背包承受的重量的时候，就不要再装了
        f(i+1, cw + items[i], items, n, w); // 当前物品装进背包
    }
}

正则表达式

正则表达式中，最重要的就是通配符，通配符结合在一起，可以表达非常丰富的语义。为了方便讲解，我假设正则表达式中只包含“*”和“?”这两种通配符，并且对这两个通配符的语义稍微做些改变，其中，“*”匹配任意多个任意字符，“?”匹配零个或者一个任意字符。

我们依次考察正则表达式中的每个字符，当是非通配符时，我们就直接跟文本的字符进行匹配，如果相同，则继续往下处理；如果不同，则回溯。如果遇到特殊字符的时候，我们就有多种处理方式了，也就是所谓的岔路口，比如“*”有多种匹配方案，可以匹配任意个文本串中的字符，我们就先随意的选择一种匹配方案，然后继续考察剩下的字符。如果中途发现无法继续匹配下去了，我们就回到这个岔路口，重新选择一种匹配方案，然后再继续匹配剩下的字符：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
public class Pattern 
{
    private boolean matched = false;
    private char[] pattern; // 正则表达式
    private int plen;       // 正则表达式长度

    public Pattern(char[] pattern, int plen) 
    {
        this.pattern = pattern;
        this.plen = plen;
    }

    public boolean match(char[] text, int tlen) 
    { 
        // 文本串及长度
        matched = false;
        rmatch(0, 0, text, tlen);
        return matched;
    }

    private void rmatch(int ti, int pj, char[] text, int tlen) 
    {
        if (matched)
        {
            return; // 如果已经匹配了，就不要继续递归了
        }
        if (pj == plen) 
        { 
            // 正则表达式到结尾了
            if (ti == tlen)
            {
                matched = true; // 文本串也到结尾了
            }
            return;
        }
        if (pattern[pj] == '*') 
        { 
            // * 匹配任意个字符
            for (int k = 0; k <= tlen-ti; ++k) 
            {
                rmatch(ti+k, pj+1, text, tlen);
            }
        } 
        else if (pattern[pj] == '?') 
        { 
            // ? 匹配 0 个或者 1 个字符
            rmatch(ti, pj+1, text, tlen);
            rmatch(ti+1, pj+1, text, tlen);
        } 
        else if (ti < tlen && pattern[pj] == text[ti]) 
        { 
            // 纯字符匹配才行
            rmatch(ti+1, pj+1, text, tlen);
        }
    }
}