旋转矩阵
点和向量,坐标系
坐标的具体取值,一是和向量本身有关,二是和坐标系的选取有关。
刚体:不光有位置,还有自身的姿态。
不要把向量与它的坐标两个概念混淆,只有当我们指定这个三维空间中的某个坐标系时,才可以谈论该向量在此坐标系下的坐标;如果我们确定了一个坐标系,也就是一个线性空间的基(e1, e2, e3),那么就可以谈论向量 a 在这组基下的坐标了: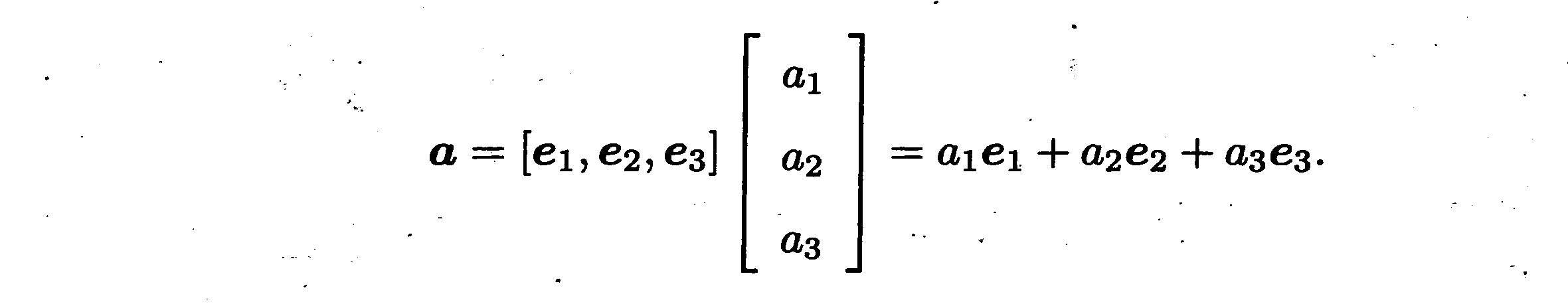
- 内积:a · b = a T b = |a||b|cos<a, b>,数量积,描述向量间的投影关系。
- 外积:a x b = a ^ b = |a||b|sin<a, b>,向量积,方向垂直于这两个向量,是两个向量张成的四边形的有向面积。
外积只对三维向量存在定义,我们还能用外积表示向量的旋转。大拇指的朝向就是旋转向量的方向,大小则由 a 和 b 的夹角决定。
坐标系间的欧氏变换
转换关系由一个矩阵 T 来描述: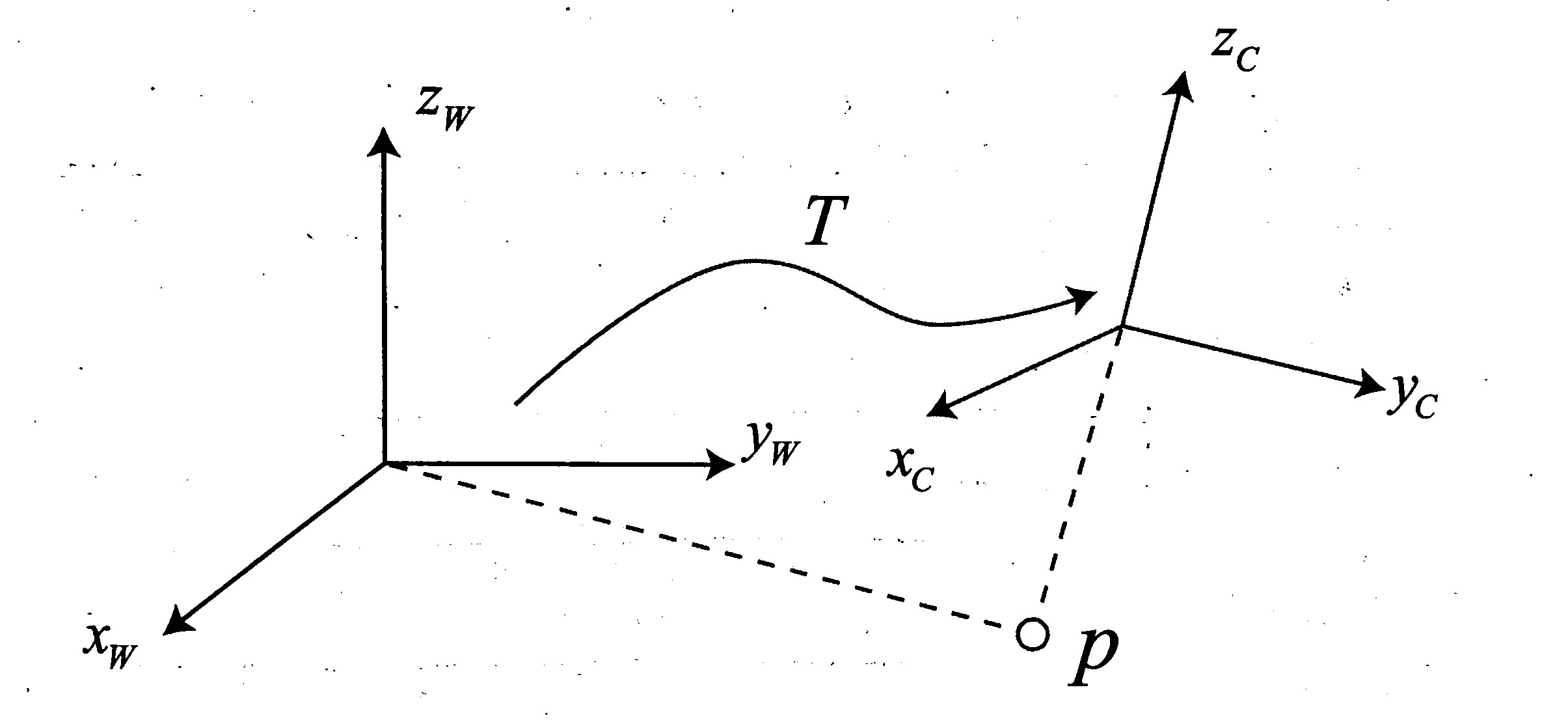
相机运动是一个刚体运动,这种变换称为欧氏变换,对于同一个向量 a ,该向量并没有随着坐标系的旋转而发生运动。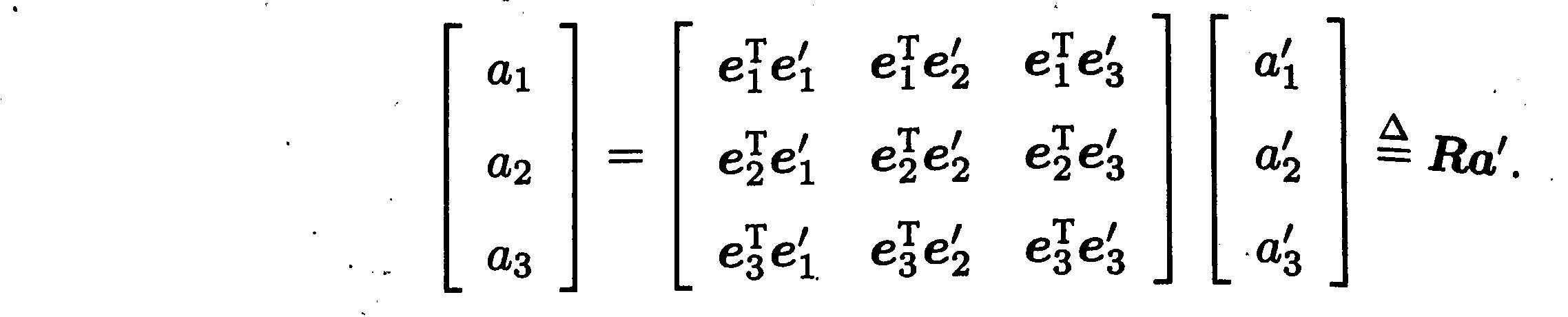
矩阵 R 描述了旋转本身,因此又称为旋转矩阵。
旋转矩阵可以描述相机的旋转,是行列式为 1 的正交矩阵,集合定义如下: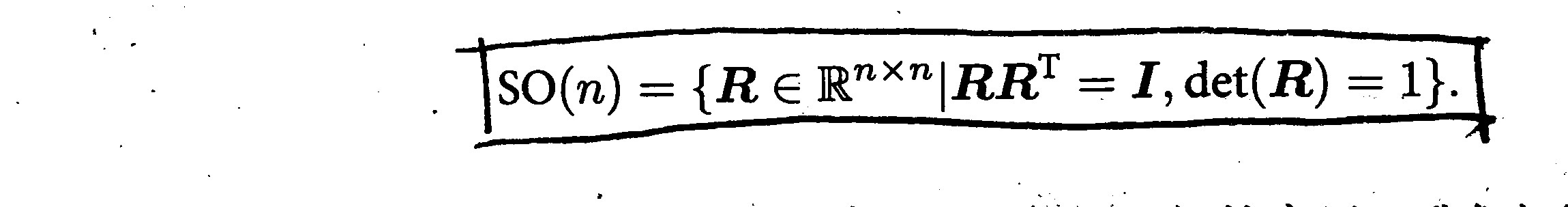
SO(3) 是特殊正交群(Special Orthogonal Group)。
正交矩阵即逆为自身转置的矩阵,R^T 刻画了一个相反的旋转。a'=Ra+t 用一个旋转矩阵 R 和一个平移向量 t 完整地描述了一个欧氏空间的坐标变换关系。
变换矩阵与齐次坐标
a'=Ra+t 的变换关系不是一个线性关系 ,在变换多次后会过于复杂。因此,我们要引入齐次坐标和变换矩阵重写式: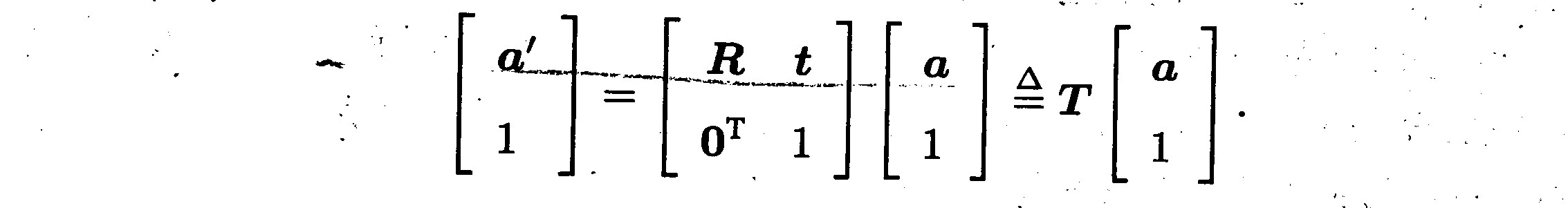
把旋转和平移写在一个矩阵里面,使得整个关系变成线性关系,矩阵 T 称为变换矩阵(Transform Matrix)。
用 4 个实数描述了一个三维向量,多了一个自由度,一个点的具体坐标值不是唯一的。如 [1, 1, 1, 1]^T 和 [2, 2, 2, 2]^T 是同一个点。
T 具有比较特别的结构:左上角为旋转矩阵,右侧为平移向量,左下角为 0 向量,右下角为 1。这种矩阵又称为特殊欧氏群(Special Euclidean Group):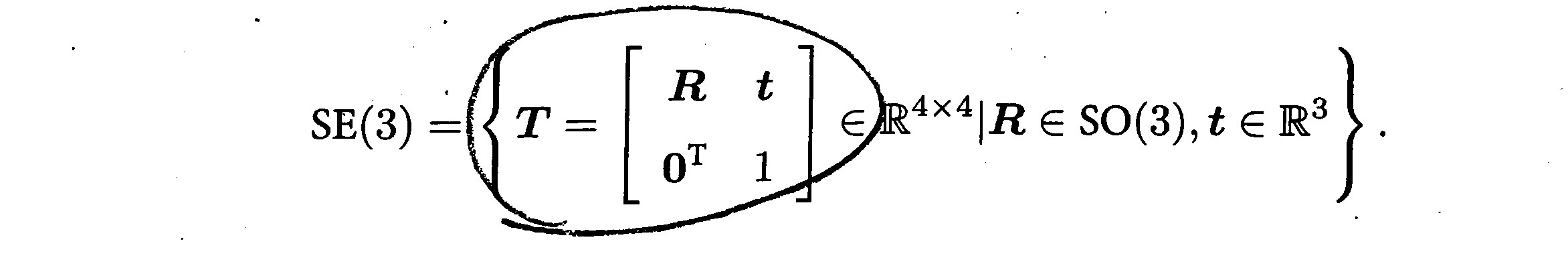
与 SO(3) 一样,求解该矩阵的逆表示一个反向的变换: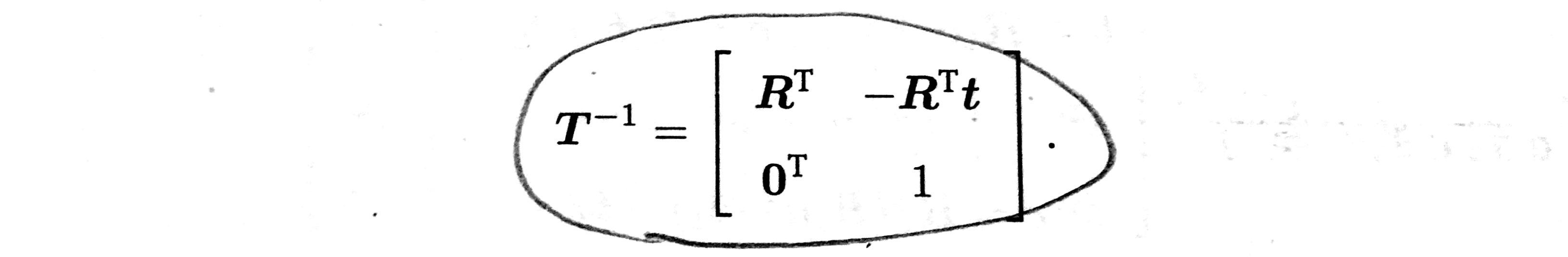
旋转可以有旋转矩阵 SO(3) 描述,平移直接由一个 R^3 向量描述。如果将平移和旋转放在一个矩阵中,就形成了变换矩阵 SE(3)。
实践:Eigen
本节讲解如何使用 Eigen 来表示矩阵、向量。
Eigen 是一个 C++ 开源线性代数库,它提供了快速的有关矩阵的线性代数运算,还包括解方程等功能。许多上层的软件库也使用 Eigen 进行矩阵运算,包括 g2o、Sophus 等。
可以输入以下命令,查找 Eigen 头文件:
1 | $ sudo updatedb |
不需要使用 target_link_libraries 将程序链接到库上,Eigen 是一个纯用头文件搭建起来的库,没有 *.so 或 *.a 那样的二进制库文件。除了使用 include_directories 指定头文件目录,我们还可以使用 find_package 命令去搜索库。
几处重要说明
- Eigen 以矩阵为基本数据单元,它是一个模板类,前三个参数为:数据类型、行、列。
- 在 Eigen 中需要指定矩阵的大小和类型,处理起来会比动态变化大小的矩阵更快一些。
- 必须显式地对矩阵类型进行转换, 否则报错:
YOU MIXED DIFFERENT NUMERIC TYPES。 - 必须保证矩阵维数的正确性,否则报错:
YOU MIXED MATRICES OF DIFFERENT SIZES。
旋转向量和欧拉角
旋转向量
旋转向量就是李代数
任意旋转都可以用一个旋转轴和一个旋转角来刻画,我们可以使用一个向量,其方向与旋转轴一致,而长度等于旋转角。这种向量称为旋转向量(或轴角,Axis-Angle)。
对于变换矩阵,我们使用一个旋转向量和一个平移向量即可表达一次变换,这时的维数正好是六维。
矩阵表示方式的缺点
- SO(3) 的旋转矩阵有 9 个量,用它表达 3 个自由度的旋转
是冗余的。同理,SE(3) 的变换矩阵用 16 个量表达了 6 自由度的变换。 - 旋转矩阵自身
带有约束:它必须是正交矩阵,且行列式为 1。变换矩阵也是如此。
旋转向量到旋转矩阵的转换
借助罗德里格斯公式(Rodrigues’s Formula):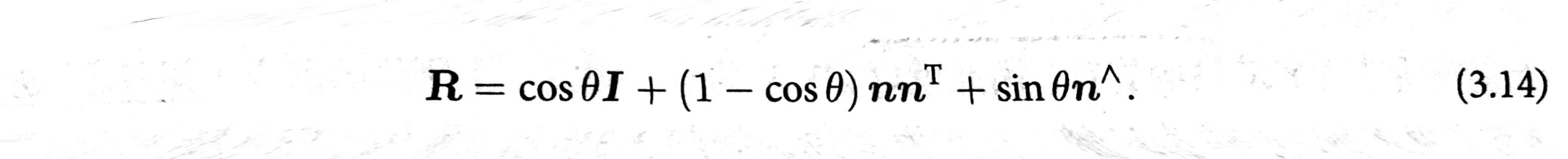
符号 ^ 是向量的反对称转换符。
旋转矩阵到旋转向量的转换
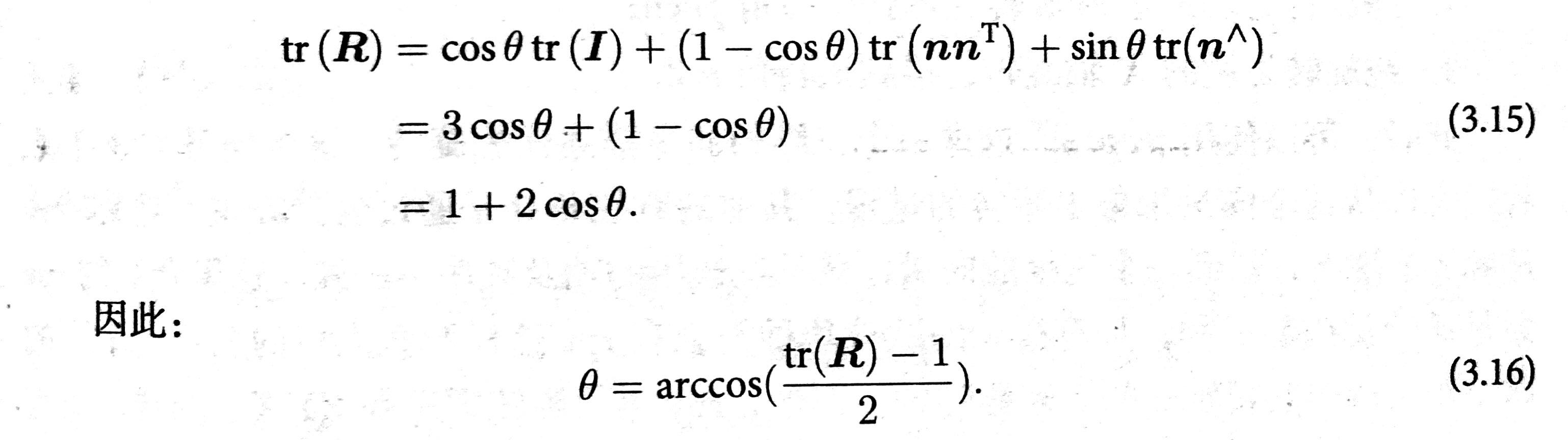
由于旋转轴上的向量在旋转后不反生改变,转轴 n 是矩阵 R 特征值 1 对应的特征向量。
欧拉角
旋转矩阵、旋转向量虽然能描述旋转,但对我们人类是非常不直观的。欧拉角提供了一种非常直观的方式来描述旋转——它使用了 3 个分离的转角。
欧拉角当中比较常用的一种,便是用“偏航-俯仰-滚转”(yaw-pitch-roll)3 个角度来描述一个旋转,等价于 ZYX 轴的旋转。
刚体朝向我们的方向为 X 轴,右侧为 Y 轴,上方为 Z 轴。
万向锁问题(Gimbal Lock)
在俯仰角为 ±90° 时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失了一个自由度。
只要想用 3 个实数表达三维旋转时,都会不可避免地碰到奇异性问题。
四元数
四元数的定义
旋转矩阵用 9 个量描述 3 自由度的旋转,具有冗余性;欧拉角和旋转向量是紧凑的,但具有奇异性。事实上,我们找不到不带奇异性的三维向量描述方式。
这有点类似于用两个坐标表示地球表面(如经度和纬度),将必定存在奇异性(纬度为 ±90° 时经度无意义)。
我们用复数集 C 表示复平面上的向量,而复数的乘法则表示复平面的旋转:例如,乘上复数 i 相当于逆时针把一个复向量旋转 90°。类似地,在表达三维空间的旋转时,也有一种类似于复数的代数:四元数(Quaternion)。四元数是一种扩展的复数,它既是紧凑的,也没有奇异性。
一个四元数 q 拥有一个实部和三个虚部,像下面这样: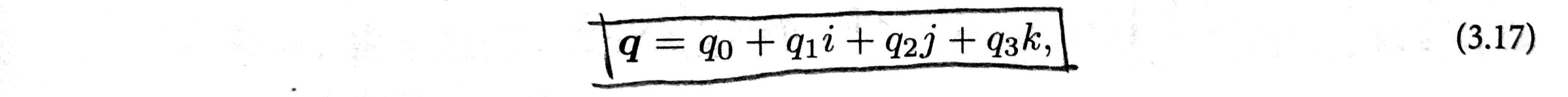
其中,I,j,k 为四元数的三个虚部。这三个虚部满足以下关系式: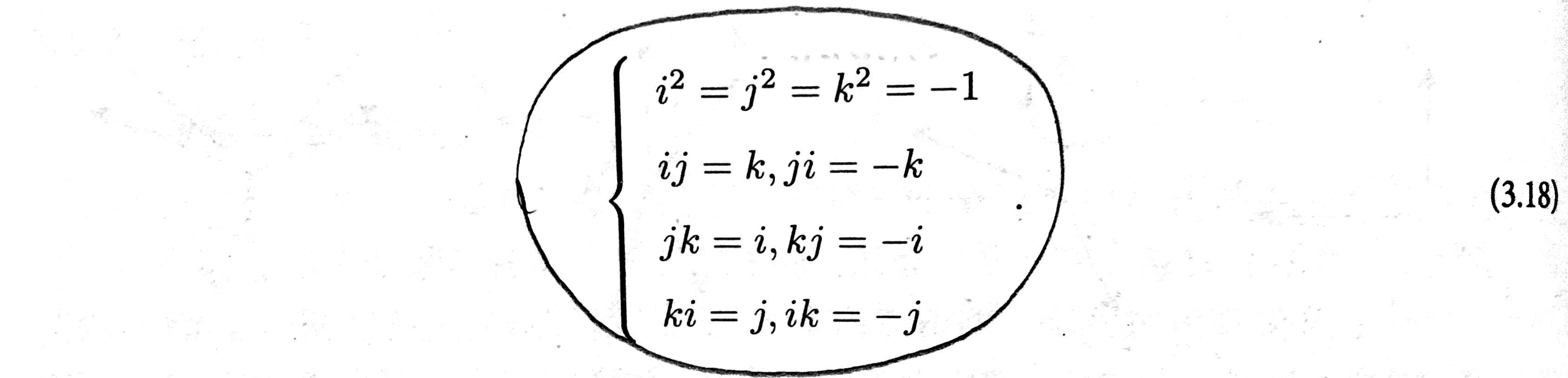
有时人们也用一个标量和一个向量来表达四元数: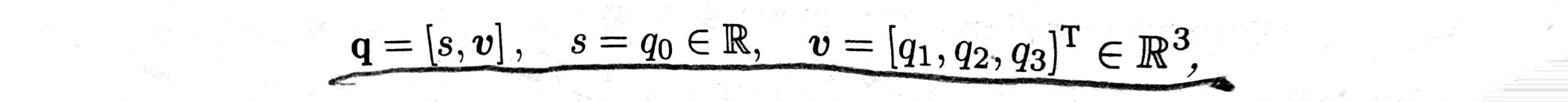
这里,s 称为四元数的实部,而 v 称为它的虚部。如果一个四元数的虚部为 0,称之为实四元数。反之,若它的实部为 0,则称之为虚四元数。
任意的旋转都可以由两个互为相反数的四元数表示。
四元数的运算
四元数和通常复数一样,可以进行一系列的运算。常见的有四则运算、数乘、点乘、求逆、求模、共轭等。
四元数与旋转向量的转换
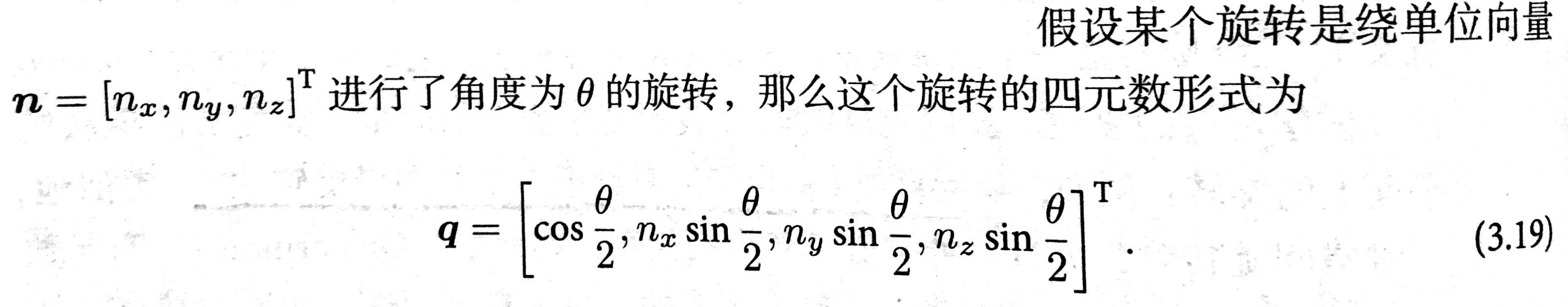
反之,亦可从单位四元数中计算出对应旋转轴与夹角: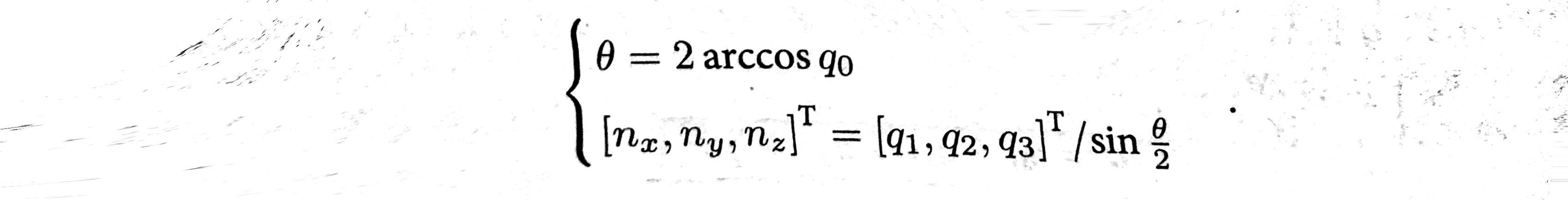
四元数与旋转矩阵的转换
现在看来把四元数转换为矩阵的最直观方法,是先把四元数 q 转换为轴角 θ 和 n,然后再根据罗德里格斯公式转换为矩阵。不过那样要计算一个 arccos 函数,代价较大。
反之,由旋转矩阵到四元数的转换如下:
无论是四元数、旋转矩阵还是轴角,它们都可以用来描述同一旋转。我们应该在实际中选择最为方便的形式,而不拘泥于某种特定的形式。
相似、仿射、射影变换
欧氏变换保持了向量的长度和夹角,相当于我们把一个刚体原封不动地进行了移动或旋转,不改变它自身的样子。而其他几种变换则会改变它的外形,它们都拥有类似的矩阵表示。
相似变换
相似变换比欧氏变换多了一个自由度,它允许物体进行均匀缩放,其矩阵表示为: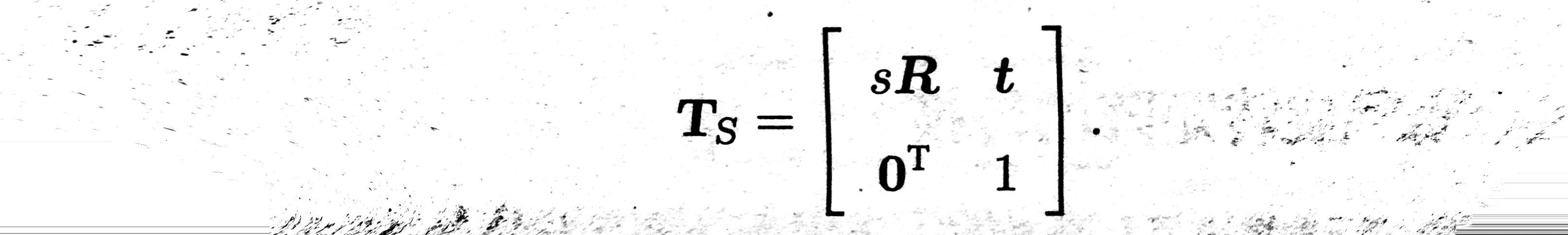
仿射变换
与欧氏变换不同的是,仿射变换只要求 A 是一个可逆矩阵,而不必是正交矩阵。经过仿射变换之后,立方体不再是方的了,但是各个面仍然是平行四边形,其矩阵形式如下: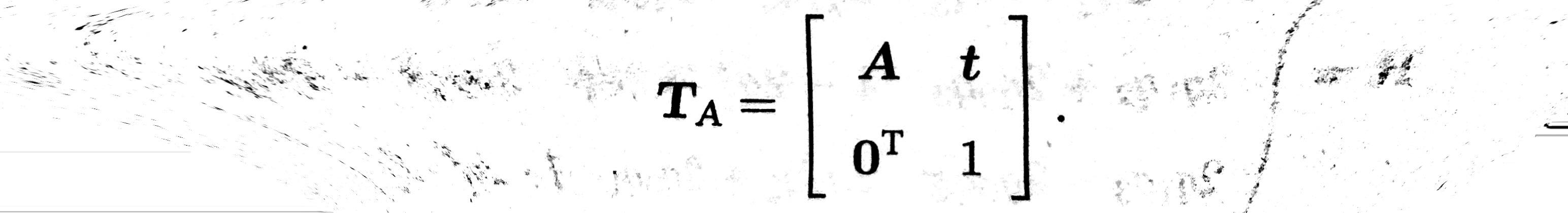
射影变换
从真实世界到相机照片的变换可以看成一个射影变换(如果相机的焦距为无穷远,那么这个变换为仿射变换)。我们可以想象一个原本方形的地板砖,在照片中是什么样子:首先,它不再是方形的。由于近大远小的关系,它甚至不是平行四边形,而是一个不规则的四边形,它的矩阵形式为: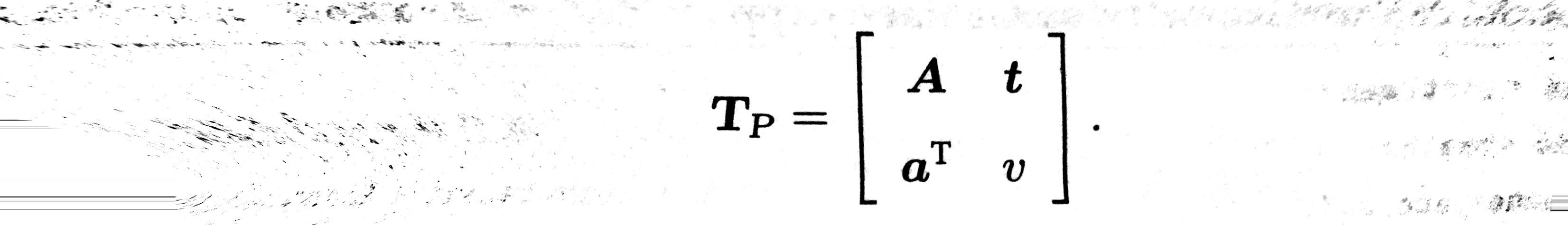
下表总结了几种变换的性质。注意在不变性质中,从上到下是有包含关系的: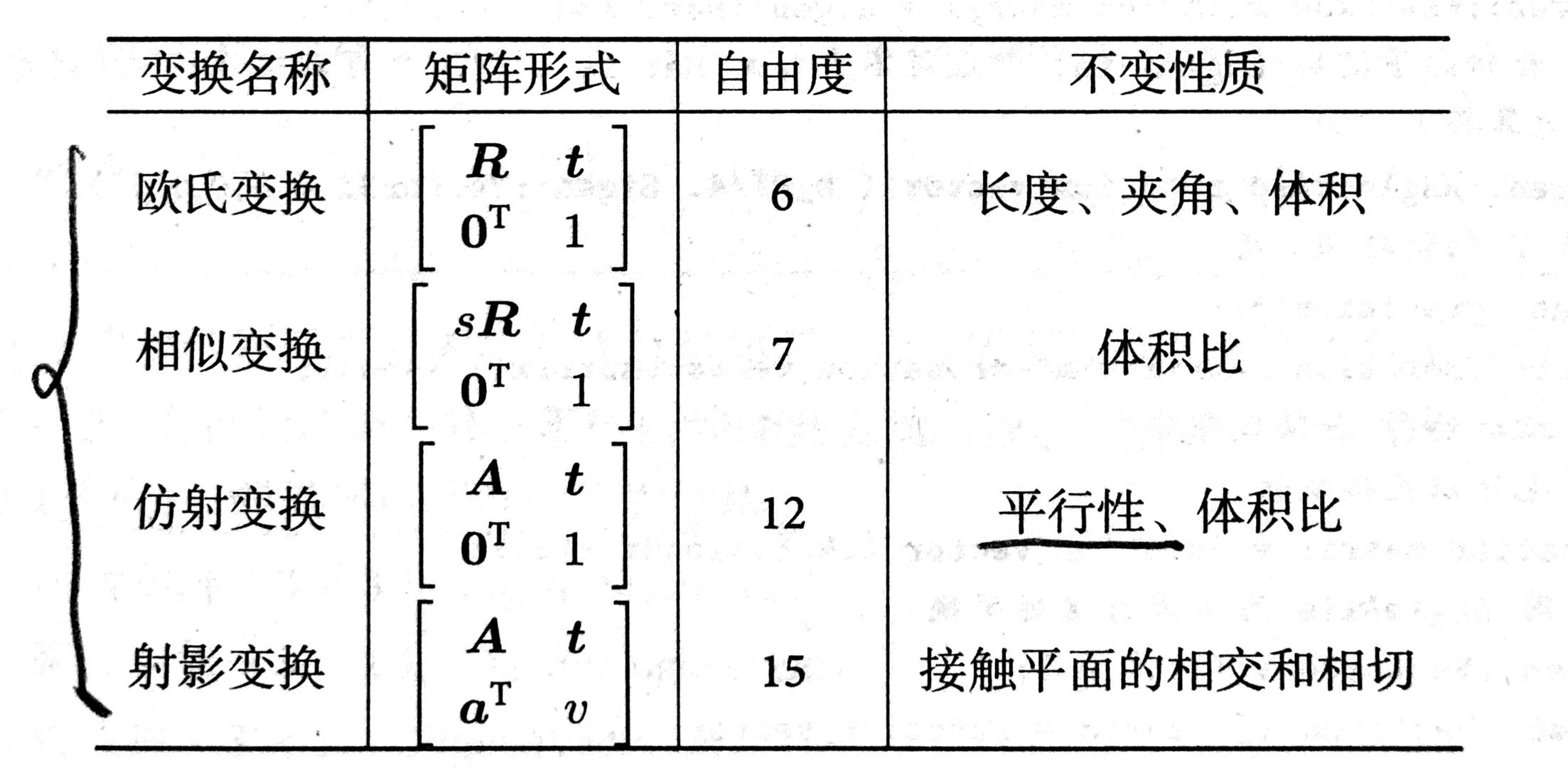
实践:Eigen 几何模块
我们将在 Eigen 中使用四元数、欧拉角和旋转矩阵,演示它们之间的变换方式。每种类型都有单精度和双精度两种数据类型(不能由编译器自动转换),下面以双精度为例,把最后的 d 改成 f,即得到单精度的数据结构:
可视化演示
我们准备了一个小程序,以可视化的形式演示了各种表达方式的异同。
实际中,我们会至少定义两个坐标系:世界坐标系和相机坐标系。在该定义下,设某个点在世界坐标系中的坐标为 Pw,在相机坐标系下为 Pc,那么:
1 | Pc = TcwPw |
这里 Tcw 表示世界坐标系到相机坐标系间的变换。或者可以用反过来的 Twc:
1 | Pw = TwcPc = Tcw^-1Pc |
如果把上面式子的 Pc 取成零向量(也就是相机坐标系的原点),那么,此时的 Pw 就是相机原点在世界坐标系下的坐标,可以从 Twc 中直接看到相机在何处(Twc 的平移部分):
1 | Pw = Twc0 = twc |
实践中使用 Tcw 更加常见,而 Twc 更为直观。