算法解释
顾名思义,分治问题由“分 (Divide)”和“治 (Conquer)”两部分组成,通过把原问题分为子问题,再将子问题进行处理合并,从而实现对原问题的求解。我们在排序章节展示的归并排序就是典型的分治问题,其中“分”即为把大数组平均分成两个小数组,通过递归实现,最终我们会得到多个长度为 1 的子数组;“治”即为把已经排好序的两个小数组合成为一个排好序的大数组,从长度为 1 的子数组开始,最终合成一个大数组。
我们也使用数学表达式来表示这个过程。定义 T(n) 表示处理一个长度为 n 的数组的时间复杂度,则归并排序的时间复杂度递推公式为 T(n) = 2T(n/2) + O(n)。其中 2T(n/2) 表示我们分成了两个长度减半的子问题,O(n) 则为合并两个长度为 n/2 数组的时间复杂度。
那么怎么利用这个递推公式得到最终的时间复杂度呢?这里我们可以利用著名的主定理 (Master Theorem) 求解: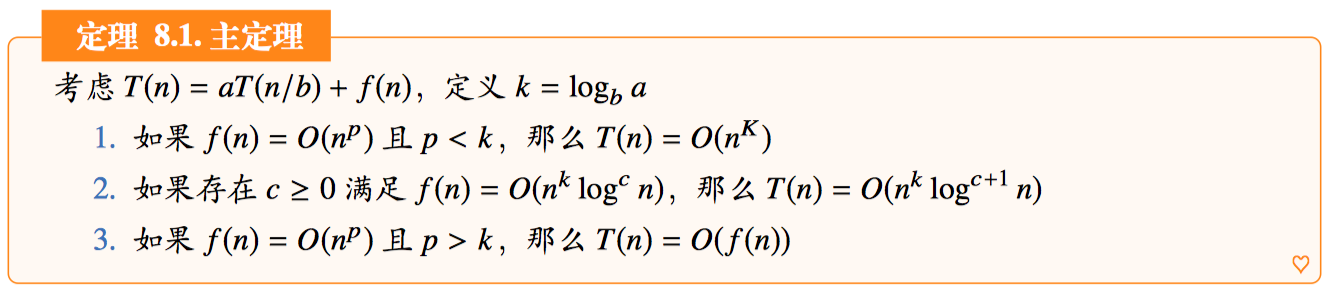
通过主定理我们可以知道,归并排序属于第二种情况,且时间复杂度为 O(nlogn),其他的分治问题也可以通过主定理求得时间复杂度。另外,自上而下的分治可以和 Memoization 结合,避免重复遍历相同的子问题;如果方便推导,也可以换用自下而上的动态规划方法求解。
表达式问题
241. Different Ways to Add Parentheses
利用分治思想,我们可以把加括号转化为:对于每个运算符号,先执行处理两侧的数学表达式,再处理此运算符号。注意边界情况,即字符串内无运算符号,只有数字。我们发现,某些被 Divide 的子字符串可能重复出现多次,因此我们可以用 Memoization 来去重。
练习
932. Beautiful Array
试着用从上到下的分治(递归)写法求解,最好加上 Memoization;再用从下到上的动态规划写法求解。
312. Burst Balloons
试着用从上到下的分治(递归)写法求解,最好加上 Memoization;再用从下到上的动态规划写法求解。