深入浅出动态规划

Posted on

算法解释

这里我们引用一下维基百科的描述：“动态规划 (DP) 在查找有很多重叠子问题的情况的最优解时有效，它将问题重新组合成子问题。为了避免多次解决这些子问题，它们的结果都逐渐被计算并被保存，从简单的问题直到整个问题都被解决。动态规划只能应用于有最优子结构的问题，最优子结构的意思是局部最优解能决定全局最优解（对有些问题这个要求并不能完全满足，故有时需要引入一定的近似）。简单地说，问题能够分解成子问题来解决。”

通俗一点来讲，动态规划和其它遍历算法（如深/广度优先搜索）都是将原问题拆成多个子问题然后求解，他们之间最本质的区别是：动态规划保存子问题的解，避免重复计算。解决动态规划问题的关键是找到状态转移方程，这样我们可以通过计算和储存子问题的解来求解最终问题。

同时，我们也可以对动态规划进行空间压缩，起到节省空间消耗的效果。在一些情况下，动态规划可以看成是带有状态记录 (Memoization) 的优先搜索。状态记录的意思为，如果一个子问题在优先搜索时已经计算过一次，我们可以把它的结果储存下来，之后遍历到该子问题的时候可以直接返回储存的结果：

  • 动态规划是自下而上的，即先解决子问题，再解决父问题。
  • 带有状态记录的优先搜索是自上而下的，即从父问题搜索到子问题，若重复搜索到同一个子问题则进行状态记录，防止重复计算。

如果题目需求的是最终状态，那么使用动态规划比较方便；如果题目需要输出所有的路径，那么使用带有状态记录的优先搜索会比较方便。

基本动态规划：一维

70. Climbing Stairs
这是十分经典的斐波那契数列题。

有的时候为了方便处理边界情况，我们可以在构造 dp 数组时多留一个位置，用来处理初始状态。本题即多留了一个第 0 阶的初始位置。

198. House Robber
我们考虑 dp[i]，此时可以抢劫的最大数量有两种可能，一种是我们选择不抢劫这个房子，此时累计的金额即为 dp[i-1]；另一种是我们选择抢劫这个房子，那么此前累计的最大金额只能是 dp[i-2]，因为我们不能够抢劫第 i-1 个房子，否则会触发警报机关。

413. Arithmetic Slices
由于我们对于 dp 数组的定义通常是以 i 结尾的、满足某些条件的子数组数量，而等差子数组可以在任意一个位置终结，所以我们需要对 dp 数组求和进行子数组统计。

基本动态规划：二维

64. Minimum Path Sum
因为每次只能向下或者向右移动，我们可以很直观地得到状态转移方程 dp[i][j] = grid[i][j] + min(dp[i][j-1], dp[i-1][j])，其中 grid 表示原数组。

如果不是很熟悉空间压缩技巧，优先尝试写出非空间压缩的解法，如果时间充裕且力所能及再进行空间压缩。

542. 01 Matrix
我们从左上到右下进行一次动态规划，再从右下到左上进行一次动态规划。两次动态规划即可完成四个方向上的查找。

221. Maximal Square
对于在矩阵内搜索正方形或长方形的题型，一种常见的做法是定义一个二维 dp 数组，其中 dp[i][j] 表示满足题目条件的、以 (i, j) 为右下角的正方形或者长方形的属性。

分割类型题

279. Perfect Squares
对于分割类型题，动态规划的状态转移方程通常并不依赖相邻的位置，而是依赖于满足分割条件的位置。

91. Decode Ways
这是一道很经典的动态规划题，难度不大但是十分考验耐心。

139. Word Break
类似于完全平方数分割问题，这道题的分割条件由集合内的字符串决定，因此在考虑每个分割位置时，需要遍历字符串集合，以确定当前位置是否可以成功分割。

1105. Filling Bookcase Shelves
令 dp[i] 表示放置第 i 本书时的最小总高度，则 dp[i] 可以是在第 i-1 本书下面重新放一排，也可以是在满足不超过前一排宽度的情况下放在前一排。

377. Combination Sum IV
令 dp[i] 表示加起来和为 i 时，满足条件的排列数量。在内循环中我们可以直接对所有合法数字进行拿取。

子序列问题

300. Longest Increasing Subsequence
对于子序列问题，第一种动态规划方法是：定义一个 dp 数组，其中 dp[i] 表示以 i 结尾的子序列的性质。在处理好每个位置后，统计一遍各个位置的结果即可得到题目要求的结果。本题还可以使用二分查找将时间复杂度降低为 O(nlogn)。我们定义一个 dp 数组，其中 dp[k] 存储长度为 k+1 的最长递增子序列的最后一个数字，注意 dp 数组最终的形式并不一定是合法的排列形式。

按照 LeetCode 的习惯，子序列 (Subsequence) 不必连续，子数组 (Subarray) 或子字符串 (Substring) 必须连续。

1143. Longest Common Subsequence
对于子序列问题，第二种动态规划方法是：定义一个 dp 数组，其中 dp[i] 表示到位置 i 为止的子序列的性质，并不必须以 i 结尾。这样 dp 数组的最后一位结果即为题目所求，不需要再对每个位置进行统计。

背包问题

背包问题是一种组合优化的 NP 完全问题：有 n 个物品和载重为 w 的背包，每个物品都有自己的重量 weight 和价值 value，求拿哪些物品可以使得背包所装下物品的总价值最大。如果限定每种物品只能选择 0 个或 1 个，则问题称为 0-1 背包问题；如果不限定每种物品的数量，则问题称为无界背包问题或完全背包问题。

我们可以用动态规划来解决背包问题。以 0-1 背包问题为例，我们可以定义一个二维数组 dp 存储最大价值，其中 dp[i][j] 表示前 i 件物品重量不超过 j 的情况下能达到的最大价值。在我们遍历到第 i 件物品时，在当前背包总载重为 j 的情况下，如果我们不将物品 i 放入背包，那么 dp[i][j] = dp[i-1][j]，即前 i 个物品的最大价值等于只取前 i-1 个物品时的最大价值；如果我们将物品 i 放入背包，假设第 i 件物品重量为 weight，价值为 value，那么我们得到 dp[i][j] = dp[i-1][j-weight] + value。我们只需在遍历过程中对这两种情况取最大值即可，总时间复杂度和空间复杂度都为 O(nw)：

1
2
3
4
5
6
7
8
9
10
11
12
13
def knapsack(weights, values, n, w):
    dp = [[0] * (w + 1) for _ in range(n + 1)]

    for i in range(1, n + 1):
        weight, value = weights[i-1], values[i-1]
        for j in range(1, w + 1):
            if j >= weight:
                dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight] + value)

            else:
                dp[i][j] = dp[i-1][j]
    
    return dp[-1][-1]

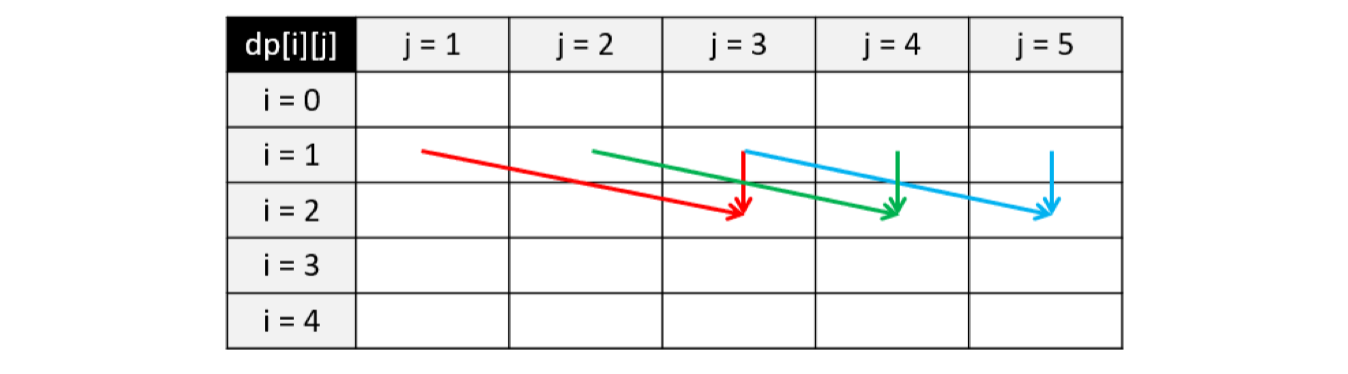
我们可以进一步对 0-1 背包进行空间优化，将空间复杂度降低为 O(w)。如图所示，假设我们目前考虑物品 i = 2，且其重量为 weight = 2，价值为 value = 3；对于背包载重 j，我们可以得到 dp[2][j] = max(dp[1][j], dp[1][j-2] + 3)。这里可以发现我们永远只依赖于上一排 i = 1 的信息，之前算过的其他物品都不需要再使用。因此我们可以去掉 dp 矩阵的第一个维度，在考虑物品 i 时变成 dp[j] = max(dp[j], dp[j-weight] + value)。这里要注意我们在遍历每一行的时候必须逆向遍历，这样才能够调用上一行物品 i-1 时 dp[j-weight] 的值；若按照从左往右的顺序进行正向遍历，则 dp[j-weight] 的值在遍历到 j 之前就已经被更新成物品 i 的值了：

1
2
3
4
5
6
7
8
9
def knapsack(weights, values, n, w):
    dp = [0] * (w + 1)

    for i in range(1, n + 1):
        weight, value = weights[i-1], values[i-1]
        for j in range(w, weight - 1, -1):
            dp[j] = max(dp[j], dp[j-weight] + value)
    
    return dp[-1]

在完全背包问题中，一个物品可以拿多次。如图上半部分所示，假设我们遍历到物品 i = 2，且其重量为 weight = 2，价值为 value = 3；对于背包载重 j = 5，最多只能装下 2 个该物品。那么我们的状态转移方程就变成了 dp[2][5] = max(dp[1][5], dp[1][3] + 3, dp[1][1] + 6)。如果采用这种方法，假设背包载重无穷大而物体的重量无穷小，我们这里的比较次数也会趋近于无穷大，远超 O(nw) 的时间复杂度。

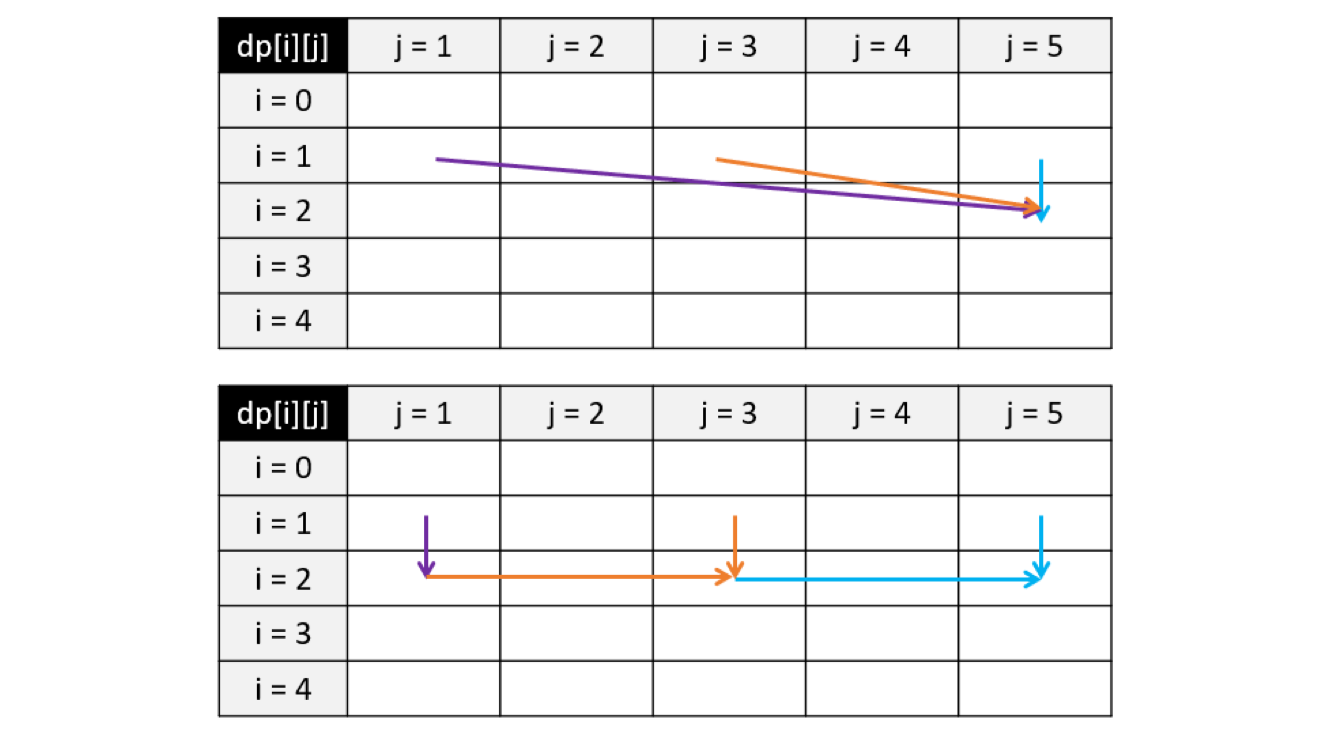
怎么解决这个问题呢？我们发现在 dp[2][3] 的时候我们其实已经考虑了 dp[1][3] 和 dp[2][1] 的情况，而在 dp[2][1] 时也已经考虑了 dp[1][1] 的情况。因此，如图下半部分所示，对于拿多个物品的情况，我们只需考虑 dp[2][3] 即可，即 dp[2][5] = max(dp[1][5], dp[2][3] + 3)。这样，我们就得到了完全背包问题的状态转移方程：dp[i][j] = max(dp[i-1][j], dp[i][j-weight] + value)，其与 0-1 背包问题的差别仅仅是把状态转移方程中的第二个 i-1 变成了 i：

1
2
3
4
5
6
7
8
9
10
11
12
13
def knapsack(weights, values, n, w):
    dp = [[0] * (w + 1) for _ in range(n + 1)]

    for i in range(1, n + 1):
        weight, value = weights[i-1], values[i-1]
        for j in range(1, w + 1):
            if j >= w:
                dp[i][j] = max(dp[i-1][j], dp[i][j-weight] + value)
            
            else:
                dp[i][j] = dp[i-1][j]
    
    return dp[-1][-1]

同样的，我们也可以利用空间压缩将时间复杂度降低为 O(w)。这里要注意我们在遍历每一行的时候必须正向遍历，因为我们需要利用当前物品在第 j-weight 列的信息：

1
2
3
4
5
6
7
8
9
def knapsack(weights, values, n, w):
    dp = [0] * (w + 1)

    for i in range(1, n + 1):
        weight, value = weights[i-1], values[i-1]
        for j in range(weight, w + 1):
            dp[j] = max(dp[j], dp[j-weight] + value)

    return dp[-1]

压缩空间时到底需要正向还是逆向遍历呢？物品和重量哪个放在外层，哪个放在内层呢？这取决于状态转移方程的依赖关系。在思考空间压缩前，不妨将状态转移矩阵画出来，方便思考如何进行空间压缩，以及压缩哪个维度更省空间。如果实在不想仔细思考，这里有个简单的口诀：0-1 背包对物品的迭代放在外层，内层的重量逆向遍历；完全背包对物品的迭代放在内层，外层的重量正向遍历。

416. Partition Equal Subset Sum
本题等价于 0-1 背包问题，设所有数字和为 sum，我们的目标是选取一部分物品，使得它们的总和为 sum/2。这道题不需要考虑价值，因此我们只需要通过一个布尔值矩阵来表示状态转移矩阵。

474. Ones and Zeroes
这是一个多维费用的 0-1 背包问题，有两个背包大小，0 的数量和 1 的数量。

322. Coin Change
因为每个硬币可以用无限多次，这道题本质上是完全背包。

字符串编辑

72. Edit Distance
类似于 LCS，当第 i 位和第 j 位对应的字符相同时，dp[i][j] 等于 dp[i-1][j-1]；当二者对应的字符不同时，修改的消耗是 dp[i-1][j-1] + 1，删除 i 位置/插入 j 位置的消耗是 dp[i-1][j] + 1，删除 j 位置/插入 i 位置的消耗是 dp[i][j-1] + 1。

650. 2 Keys Keyboard
不同于以往通过加减实现的动态规划，这里需要乘除法来计算位置，因为粘贴操作是倍数增加的。我们使用一个一维数组 dp，其中位置 i 表示延展到长度 i 的最少操作次数，因此我们可以得到递推公式 dp[i] = dp[j] + dp[i/j]。

股票交易

股票交易类问题通常可以用动态规划来解决。对于稍微复杂一些的股票交易类问题，比如需要冷却时间或者交易费用，则可以用通过动态规划实现的状态机来解决。

121. Best Time to Buy and Sell Stock
我们可以遍历一遍数组，在每一个位置 i 时，记录 i 位置之前所有价格中的最低价格，然后将当前的价格作为售出价格，查看当前收益是不是最大收益即可。

188. Best Time to Buy and Sell Stock IV
如果 k 小于总天数的一半，我们可以建立两个动态规划数组 buy 和 sell，对于每天的股票价格，buy[j] 表示在第 j 次买入时的最大收益，sell[j] 表示在第 j 次卖出时的最大收益。

309. Best Time to Buy and Sell Stock with Cooldown
我们可以使用状态机来解决这类复杂的状态转移问题，通过建立多个状态以及它们的转移方式，我们可以很容易地推导出各个状态的转移方程。如图所示，我们可以建立四个状态来表示带有冷却的股票交易，以及它们的之间的转移方式：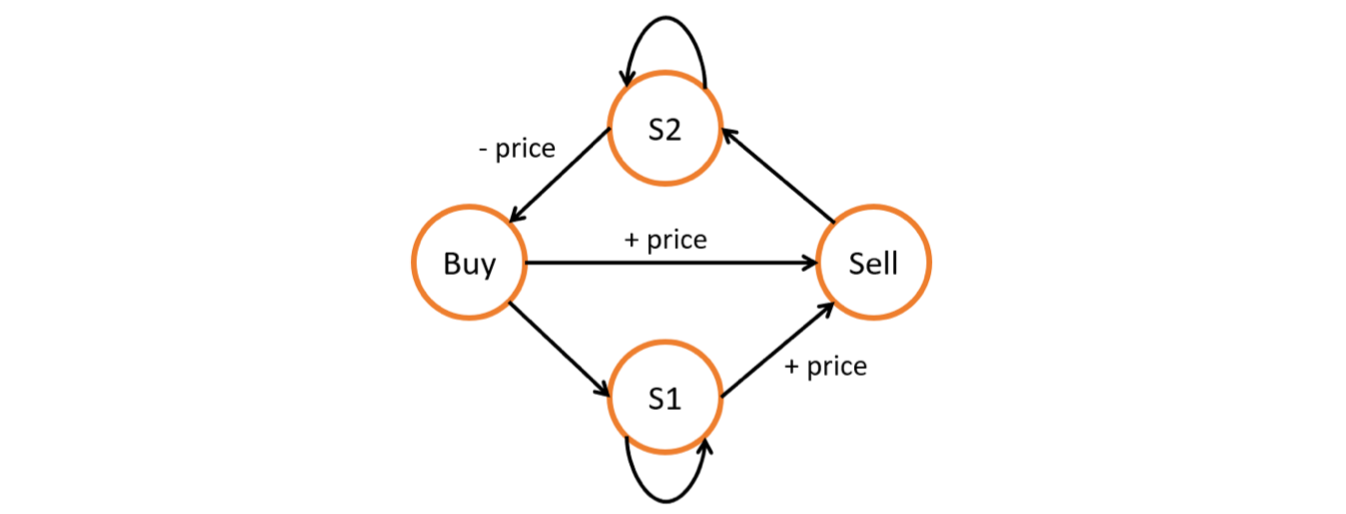

练习

213. House Robber II
强盗抢劫题目的 follow-up，如何处理环形数组呢？

53. Maximum Subarray
经典的一维动态规划题目，试着把一维空间优化为常量吧。

343. Integer Break
分割类型题，先尝试用动态规划求解，再思考是否有更简单的解法。

583. Delete Operation for Two Strings
最长公共子序列的变种题。

646. Maximum Length of Pair Chain
最长递增子序列的变种题，同样的，尝试用二分进行加速。

10. Regular Expression Matching
正则表达式匹配，非常考验耐心。需要根据正则表达式的不同情况，即字符、星号、点号等分情况讨论。

376. Wiggle Subsequence
最长摆动子序列，通项公式比较特殊，需要仔细思考。

494. Target Sum
如果告诉你这道题是 0-1 背包，你是否会有一些思路？

714. Best Time to Buy and Sell Stock with Transaction Fee
建立状态机，股票交易类问题就会迎刃而解。