四两拨千斤的位运算，比如：剥离最右边的 1、将最右边的 1 置 0 等等。更多技巧可以参考 Low Level Bit Hacks。

Bitwise XOR returns 0 (false) if both bits are the same and returns 1 (true) otherwise. In other words, it only returns 1 if exactly one bit is set to 1 out of the two bits in comparison: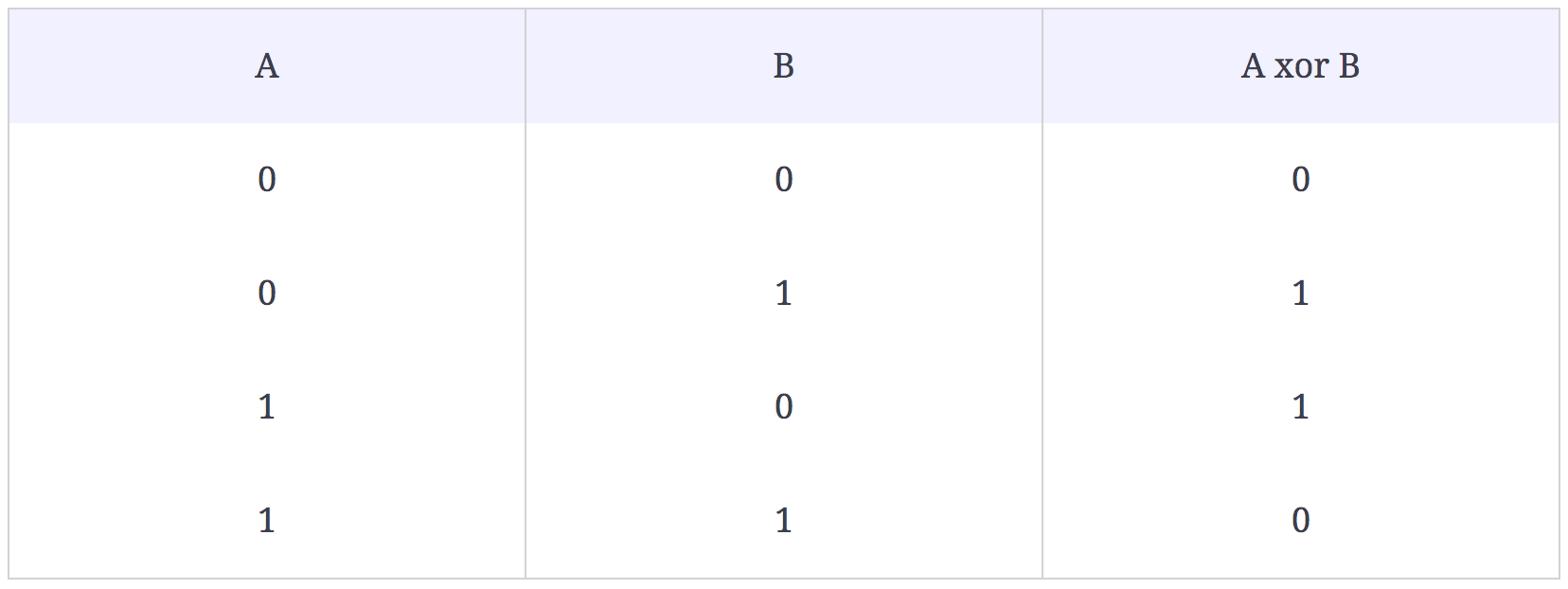

It is surprising to know the approaches that the XOR operator enables us to solve certain problems. For example, let’s take a look at the following problem:

Given an array of n-1 integers in the range from 1 to n, find the one number that is missing from the array.

Example:

1
2

Input: 1, 5, 2, 6, 4
Answer: 3

A straight forward approach to solve this problem can be:

1. Find the sum of all integers from 1 to n; let’s call it: s1.
2. Subtract all the numbers in the input array from s1; this will give us the missing number.

无处不在的二分思想。往往通过外部变量 track 中间结果，元素不是 distinct 时需要单独处理。有时仅为解法的一小步，bisect_left 第一个大于等于；bisect_right 第一个大于。

As we know, whenever we are given a sorted array or linked list or matrix, and we are asked to find a certain element, the best algorithm we can use is binary search.

This pattern describes an efficient way to handle all problems involving Binary Search. We will go through a set of problems that will help us build an understanding of this pattern so that we can apply this technique to other problems we might come across in the interviews.

Snippets

1
2
3
4
5
6
7
8
9
10
11
12

lo, hi = 0, len(nums) - 1
while lo <= hi:
    mid = lo + ((hi - lo) >> 1)
    if nums[mid] >= target:
        if mid == 0 or nums[mid-1] < target:  # find leftmost element
            return mid
        
        hi = mid - 1
    else:
        lo = mid + 1

return len(nums)  # all less

LeetCode

704. Binary Search
35. Search Insert Position
744. Find Smallest Letter Greater Than Target
34. Find First and Last Position of Element in Sorted Array
702. Search in a Sorted Array of Unknown Size
270. Closest Binary Search Tree Value
852. Peak Index in a Mountain Array
1095. Find in Mountain Array
33. Search in Rotated Sorted Array
153. Find Minimum in Rotated Sorted Array

使用 BFS 解决一系列排列、组合问题。基本上对 queue 进行迭代就可以了（需要 popleft 时选择 deque），但有时需要用到递归。

A huge number of coding interview problems involve dealing with Permutations and Combinations of a given set of elements. This pattern describes an efficient breadth-first search approach to handle all these problems.

Snippets

1
2
3
4
5
6
7
8
9
10
11
12

"""Iteration"""
queue = deque([[]])
for num in sorted(nums):  # handle duplicates
    for _ in range(len(queue)):
        item = queue.popleft()
        cand = item + [num]
        if cand not in queue:
            queue.append(cand)
        
        queue.append(item)

return queue

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

"""Recursion"""
@cache
def build(start, end):
    if start > end:
        return [None]

    trees = []
    for val in range(start, end + 1):
        # divide & conquer
        l = build(start, val - 1)
        r = build(val + 1, end)

        for x in l:
            for y in r:
                root = TreeNode(val)
                root.left = x
                root.right = y
                trees.append(root)

    return trees

return build(1, n)

LeetCode

78. Subsets
90. Subsets II
46. Permutations
784. Letter Case Permutation
22. Generate Parentheses
320. Generalized Abbreviation
241. Different Ways to Add Parentheses
95. Unique Binary Search Trees II
96. Unique Binary Search Trees

大多是 max_heap 和 min_heap 的配合使用。在用索引获取堆顶元素时，注意保证 heap 非空。

In many problems, where we are given a set of elements such that we can divide them into two parts. To solve the problem, we are interested in knowing the largest element in one part and the smallest element in the other part. This pattern is an efficient approach to solve such problems.

This pattern uses Two Heaps to solve these problems; A max heap to find the largest element and a min heap to find the smallest element.

Snippets

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

class MedianFinder:
    def __init__(self):
        self.max_heap = []
        self.min_heap = []

    def add_num(self, num: int) -> None:
        if not self.max_heap or num <= -self.max_heap[0]:
            heappush(self.max_heap, -num)
        else:
            heappush(self.min_heap, num)
        
        # rebalance
        if len(self.max_heap) > len(self.min_heap) + 1:
            heappush(self.min_heap, -heappop(self.max_heap))
        if len(self.min_heap) > len(self.max_heap):
            heappush(self.max_heap, -heappop(self.min_heap))

    def find_median(self) -> float:
        if len(self.max_heap) == len(self.min_heap):
            return (-self.max_heap[0] + self.min_heap[0]) / 2
        
        return -self.max_heap[0]

LeetCode

295. Find Median from Data Stream
480. Sliding Window Median
502. IPO
436. Find Right Interval

重点掌握左右子树相关和不相关时，两种递归代码的写法。

This pattern is based on the Depth-First Search (DFS) technique to traverse a tree.

We will be using recursion (or we can also use a stack for the iterative approach) to keep track of all the previous (parent) nodes while traversing. This also means that the space complexity of the algorithm will be O(H), where “H” is the maximum height of the tree.

Snippets

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

"""L&R Unrelated"""
def dfs(root, path):
    if not root:
        return
    
    path = path + [root.val]
    if not root.left and not root.right and sum(path) == targetSum:
        ans.append(path)
    
    dfs(root.left, path)
    dfs(root.right, path)

ans = []
dfs(root, [])

return ans

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

"""L&R Related"""
def dfs(root):
    if not root:
        return 0
    
    l = max(0, dfs(root.left))
    r = max(0, dfs(root.right))

    nonlocal ans
    ans = max(ans, l + r + root.val)

    return max(l, r) + root.val

ans = root.val
dfs(root)

return ans

LeetCode

112. Path Sum
113. Path Sum II
129. Sum Root to Leaf Numbers
1430. Check If a String Is a Valid Sequence from Root to Leaves Path in a Binary Tree
437. Path Sum III
543. Diameter of Binary Tree
124. Binary Tree Maximum Path Sum