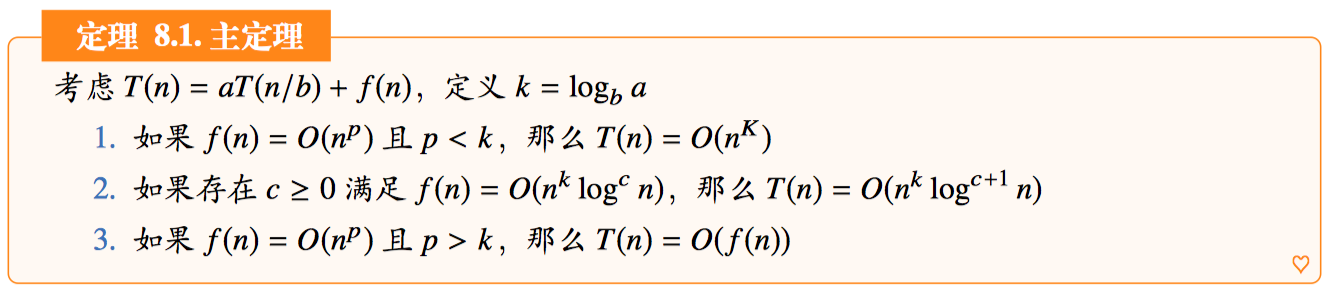引言

字符串可以看成是字符组成的数组。由于字符串是程序里经常需要处理的数据类型，因此有很多针对字符串处理的题目。

字符串比较

242. Valid Anagram
我们可以利用哈希表或者数组统计两个数组中每个数字出现的频次，若频次相同，则说明它们包含的字符完全相同。

205. Isomorphic Strings
我们可以将问题转化一下：记录两个字符串每个位置的字符第一次出现的位置，如果两个字符串中相同位置的字符与它们第一次出现的位置一样，那么这两个字符串同构。

647. Palindromic Substrings
我们可以从字符串的每个位置开始，向左向右延长，判断存在多少以当前位置为中轴的回文子字符串。

696. Count Binary Substrings
从左往右遍历数组，记录和当前位置数字相同且连续的长度，以及其之前连续的不同数字的长度。若不同数字的连续长度大于等于当前数字的连续长度，则说明存在一个且只存在一个以当前数字结尾的满足条件的子字符串。

C++ STL

在刷题时，我们几乎一定会用到各种数据结构来辅助我们解决问题，因此我们必须熟悉各种数据结构的特点。C++ STL 提供的数据结构包括（实际底层细节可能因编译器而异）：

• Sequence Containers：维持顺序的容器：
  • vector：动态数组，是我们最常使用的数据结构之一，用于 O(1) 的随机读取。因为大部分算法的时间复杂度都会大于 O(n)，因此我们经常新建 vector 来存储各种数据或中间变量。因为在尾部增删的复杂度是 O(1)，我们也可以把它当作 stack 来用。
  • list：双向链表，也可以当作 stack 和 queue 来使用。由于 LeetCode 的题目多用 Node 来表示链表，且链表不支持快速随机读取，因此我们很少用到这个数据结构（LRU 除外）。
  • deque：双端队列，这是一个非常强大的数据结构，既支持 O(1) 随机读取，又支持 O(1) 时间的头部增删和尾部增删（因此可以当作 stack 和 queue 来使用），不过有一定的额外开销。
  • array：固定大小的数组，一般在刷题时我们不使用。
  • forward_list：单向链表，一般在刷题时我们不使用。
• Container Adaptors：基于其它容器实现的容器：
  • stack：后入先出的数据结构，默认基于 deque 实现。stack 常用于深度优先搜索、一些字符串匹配问题以及单调栈问题。
  • queue：先入先出的数据结构，默认基于 deque 实现。queue 常用于广度优先搜索。
  • priority_queue：最大值先出的数据结构，默认基于 vector 实现堆结构。它可以在 O(nlogn) 的时间排序数组、O(logn) 的时间插入任意值、O(logn) 的时间删除最大值、O(1) 的时间获得最大值。priority_queue 常用于维护数据结构并快速获取最大值，并且可以自定义比较函数，比如通过存储负值或者更改比小函数为比大函数，即可实现最小值先出。

常用技巧

位运算是算法题里比较特殊的一种类型，它们利用二进制位运算的特性进行一些奇妙的优化和计算。常用的位运算符号包括：“∧ 按位异或”、“& 按位与”、“| 按位或”、“~ 取反”、“<< 算术左移”和“>> 算术右移”。以下是一些常见的位运算特性，其中 0s 和 1s 分别表示只由 0 或 1 构成的二进制数字：

除此之外，n & (n - 1) 可以去除 n 的位级表示中最低的那一位，例如对于二进制表示 11110100，减去 1 得到 11110011，这两个数按位与得到 11110000。n & -n 可以得到 n 的位级表示中最低的那一位，例如对于二进制表示 11110100，取负得到 00001100，这两个数按位与得到 00000100。还有更多的并不常用的技巧，若读者感兴趣可以自行研究，这里不再赘述。

引言

对于 LeetCode 上数量不少的数学题，我们尽量将其按照类型划分讲解。然而很多数学题的解法并不通用，我们也很难在几道题里把所有的套路讲清楚，因此我们只选择了几道经典或是典型的题目，供大家参考。

公倍数与公因数

利用辗转相除法，我们可以很方便地求得两个数的最大公因数 (GCD)；将两个数相乘再除以最大公因数即可得到最小公倍数 (LCM)。进一步地，我们也可以通过扩展欧几里得算法，在求得 a 和 b 最大公因数的同时，也得到它们的系数 x 和 y，从而使 ax + by = gcd(a, b)：

1
2
3
4
5
6
7
8
9

def gcd_extended(a, b):
    if a == 0:
        return b, 0, 1
    
    gcd, x1, y1 = gcd_extended(b % a, a)
    x = y1 - (b // a) * x1
    y = x1

    return gcd, x, y

算法解释

顾名思义，分治问题由“分 (Divide)”和“治 (Conquer)”两部分组成，通过把原问题分为子问题，再将子问题进行处理合并，从而实现对原问题的求解。我们在排序章节展示的归并排序就是典型的分治问题，其中“分”即为把大数组平均分成两个小数组，通过递归实现，最终我们会得到多个长度为 1 的子数组；“治”即为把已经排好序的两个小数组合成为一个排好序的大数组，从长度为 1 的子数组开始，最终合成一个大数组。

我们也使用数学表达式来表示这个过程。定义 T(n) 表示处理一个长度为 n 的数组的时间复杂度，则归并排序的时间复杂度递推公式为 T(n) = 2T(n/2) + O(n)。其中 2T(n/2) 表示我们分成了两个长度减半的子问题，O(n) 则为合并两个长度为 n/2 数组的时间复杂度。

那么怎么利用这个递推公式得到最终的时间复杂度呢？这里我们可以利用著名的主定理 (Master Theorem) 求解：

通过主定理我们可以知道，归并排序属于第二种情况，且时间复杂度为 O(nlogn)，其他的分治问题也可以通过主定理求得时间复杂度。另外，自上而下的分治可以和 Memoization 结合，避免重复遍历相同的子问题；如果方便推导，也可以换用自下而上的动态规划方法求解。