BF 算法

BF（Brute Force）算法，中文叫作暴力匹配算法，也叫朴素匹配算法。从名字可以看出，这种算法的字符串匹配方式很“暴力”，当然也就会比较简单、好懂，但相应的性能也不高。我们在字符串 A 中查找字符串 B，那字符串 A 就是主串，字符串 B 就是模式串。我们把主串的长度记作 n，模式串的长度记作 m。因为我们是在主串中查找模式串，所以 n>m。

作为最简单、最暴力的字符串匹配算法，BF 算法的思想可以用一句话来概括，那就是，我们在主串中，检查起始位置分别是 0, 1, 2, n-m 且长度为 m 的 n-m+1 个子串，看有没有跟模式串匹配的：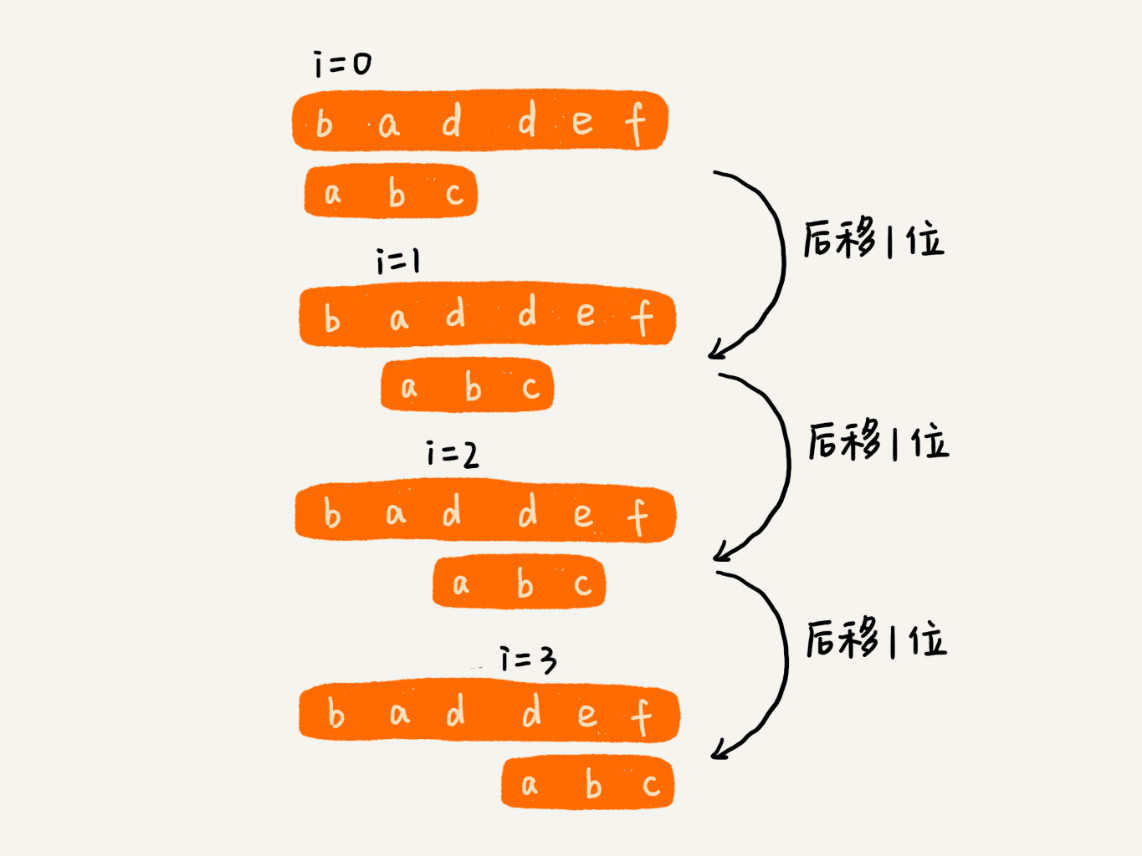

从上面的算法思想和例子，我们可以看出，在极端情况下，比如主串是“aaaaa…aaaaaa”，模式串是“aaaaab”。我们每次都比对 m 个字符，要比对 n-m+1 次，所以，这种算法的最坏情况时间复杂度是 O(n*m)。尽管理论上，BF 算法的时间复杂度很高，是 O(n*m)，但在实际的开发中，它却是一个比较常用的字符串匹配算法。原因有两点：

1. 实际的软件开发中，大部分情况下，模式串和主串的长度都不会太长。而且每次模式串与主串中的子串匹配的时候，当中途遇到不能匹配的字符的时候，就可以就停止了，不需要把 m 个字符都比对一下。所以，尽管理论上的最坏情况时间复杂度是 O(n*m)，但是，统计意义上，大部分情况下，算法执行效率要比这个高很多；
2. 朴素字符串匹配算法思想简单，代码实现也非常简单。简单意味着不容易出错，如果有 bug 也容易暴露和修复。在工程中，在满足性能要求的前提下，简单是首选；

什么是“搜索”算法？

我们知道，算法是作用于具体数据结构之上的，广度优先搜索算法和深度优先搜索算法都是基于“图”这种数据结构的。这是因为，图这种数据结构的表达能力很强，大部分涉及搜索的场景都可以抽象成图。图上的搜索算法，最直接的理解就是，在图中找出从一个顶点出发，到另一个顶点的路径。具体方法有很多，比如下面的两种最简单、最“暴力”的广度优先、深度优先搜索，还有 A*、IDA* 等启发式搜索算法。

我这里先给出图的代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

public class Graph 
{ 
    // 无向图
    private int v;                     // 顶点的个数
    private LinkedList<Integer> adj[]; // 邻接表

    public Graph(int v) 
    {
        this.v = v;
        adj = new LinkedList[v];
        for (int i=0; i<v; ++i) 
        {
            adj[i] = new LinkedList<>();
        }
    }

    public void addEdge(int s, int t) 
    { 
        // 无向图一条边存两次
        adj[s].add(t);
        adj[t].add(s);
    }
}

如何理解“图”？

图（Graph）和树比起来，这是一种更加复杂的非线性表结构。我们知道，树中的元素我们称为节点，图中的元素我们就叫做顶点（Vertex）。从我画的图中可以看出来，图中的一个顶点可以与任意其他顶点建立连接关系。我们把这种建立的关系叫做边（Edge）：

我们生活中就有很多符合图这种结构的例子。比如，社交网络就是一个非常典型的图结构。我们就拿微信举例子吧。我们可以把每个用户看作一个顶点。如果两个用户之间互加好友，那就在两者之间建立一条边。所以，整个微信的好友关系就可以用一张图来表示。其中，每个用户有多少个好友，对应到图中，就叫做顶点的度（Degree），就是跟顶点相连接的边的条数。

实际上，微博的社交关系跟微信还有点不一样，或者说更加复杂一点。微博允许单向关注，如果用户 A 关注了用户 B，我们就在图中画一条从 A 到 B 的带箭头的边，来表示边的方向。如果用户 A 和用户 B 互相关注了，那我们就画一条从 A 指向 B 的边，再画一条从 B 指向 A 的边。我们把这种边有方向的图叫做有向图。以此类推，我们把边没有方向的图就叫做无向图：

无向图中有“度”这个概念，表示一个顶点有多少条边。在有向图中，我们把度分为入度（In-degree）和出度（Out-degree）。顶点的入度，表示有多少条边指向这个顶点；顶点的出度，表示有多少条边是以这个顶点为起点指向其他顶点。对应到微博的例子，入度就表示有多少粉丝，出度就表示关注了多少人。

堆的应用一：优先级队列

优先级队列，顾名思义，它首先应该是一个队列。不过，在优先级队列中，数据的出队顺序不是先进先出，而是按照优先级来，优先级最高的，最先出队。一个堆就可以看作一个优先级队列，很多时候，它们只是概念上的区分而已。往优先级队列中插入一个元素，就相当于往堆中插入一个元素；从优先级队列中取出优先级最高的元素，就相当于取出堆顶元素。

优先级队列的应用场景非常多。比如，赫夫曼编码、图的最短路径、最小生成树算法等等。不仅如此，很多语言中，都提供了优先级队列的实现，比如，Java 的 PriorityQueue，C++ 的 priority_queue 等。只讲这些应用场景比较空泛，现在，我举两个具体的例子：

1. 合并有序小文件：
   假设我们有 100 个小文件，每个文件的大小是 100MB，每个文件中存储的都是有序的字符串。我们希望将这些 100 个小文件合并成一个有序的大文件。我们用数组这种数据结构，来存储从小文件中取出来的字符串。每次从数组中取最小字符串，都需要循环遍历整个数组，显然，这不是很高效。
   这里就可以用到优先级队列，也可以说是堆。我们将从小文件中取出来的字符串放入到小顶堆中，那堆顶的元素，也就是优先级队列队首的元素，就是最小的字符串。我们将这个字符串放入到大文件中，并将其从堆中删除。然后再从小文件中取出下一个字符串，放入到堆中。循环这个过程，就可以将 100 个小文件中的数据依次放入到大文件中。我们知道，删除堆顶数据和往堆中插入数据的时间复杂度都是 O(logn)，n 表示堆中的数据个数，这里就是 100，比原来数组存储的方式高效了很多；

如何理解“堆”？

堆是一种特殊的树。我罗列了两点要求，只要满足这两点，它就是一个堆：

• 堆是一个完全二叉树；
• 堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值；

对于每个节点的值都大于等于子树中每个节点值的堆，我们叫做大顶堆。对于每个节点的值都小于等于子树中每个节点值的堆，我们叫做小顶堆：

其中第 1 个和第 2 个是大顶堆，第 3 个是小顶堆，第 4 个不是堆。除此之外，从图中还可以看出来，对于同一组数据，我们可以构建多种不同形态的堆。